
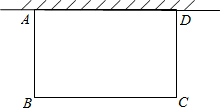
 在广元市开展的“双创”活动中,某居民小区要在一块靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园一边靠墙,另三边总长为40m的栅栏(如图所示).当BC的长为多少米时,矩形ABCD的面积为168m2?
在广元市开展的“双创”活动中,某居民小区要在一块靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园一边靠墙,另三边总长为40m的栅栏(如图所示).当BC的长为多少米时,矩形ABCD的面积为168m2? 分析 可设出花园的一边,然后根据矩形的面积=长×宽,用未知数表示出花园的面积,要求花园的面积能否达到168平方米,列出方程求解即可;
解答 解:(1)设BC长为xm(0<x≤15),则AB的长为$\frac{40-x}{2}$m,依题意,得:
$\frac{40-x}{2}$•x=168,
解得x1=20-2$\sqrt{6}$,x2=20+2$\sqrt{6}$(不合题意舍去),
答:BC的长为多(20-2$\sqrt{6}$)时,矩形ABCD的面积为168m2.
点评 本题考查了一元二次方程的运用,是一道数形结合试题.要读清题意,熟记一元二次方程根与系数的关系.读懂题意,找到等量关系准确的列出方程是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
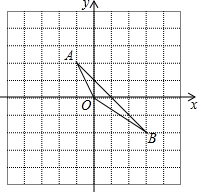 已知点A、B在平面直角坐标系中的位置如图所示,将△AOB向下平移2个单位长度,在向左平移2个单位.
已知点A、B在平面直角坐标系中的位置如图所示,将△AOB向下平移2个单位长度,在向左平移2个单位.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在数轴上有A,B两点,点A在点B的左侧,已知点B对应的数为2,点A对应的数为a.
如图,在数轴上有A,B两点,点A在点B的左侧,已知点B对应的数为2,点A对应的数为a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com