
【题目】将下列推证过程补充完整. 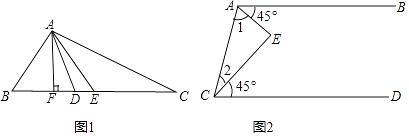
(1)如图1,在△ABC中,AE是中线,AD是角平分线,AF是高.
①BE== ![]() ;
;
②∠BAD== ![]() ;
;
③∠AFB==90°;
④S△ABC= .
(2)如图2,AB∥CD,∠BAE=∠DCE=45°,
∵AB∥CD
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= .
【答案】
(1)CE;BC;∠CAD;∠BAC;∠AFC;![]() BC?AF
BC?AF
(2)180°;90°;90°
【解析】解:(1)①BE=CE= ![]() BC;
BC;
②∠BAD=∠CAD= ![]() ∠BAC;
∠BAC;
③∠AFB=∠AFC=90°;
④S△ABC= ![]() BCAF;(2)∵AB∥CD,
BCAF;(2)∵AB∥CD,
∴∠1+45°+∠2+45°=180°,
∴∠1+∠2=90°,
∴∠E=90°.
所以答案是:(1)CE,BC;∠CAD,∠BAC;∠AFC; ![]() BCAF;(2)180°,90°,90°.
BCAF;(2)180°,90°,90°.
【考点精析】关于本题考查的平行线的性质和三角形的“三线”,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°. 求小岛B到河边公路AD的距离.
(参考数据:sin37°≈ 0.60,cos37° ≈ 0.80,tan37° ≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC的三条内角平分线为AE,BF,CG,下面的说法中正确的个数有( )
①△ABC的内角平分线上的点到三边距离相等
②三角形的三条内角平分线交于一点
③三角形的内角平分线位于三角形的内部
④三角形的任一内角平分线将三角形分成面积相等的两部分.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
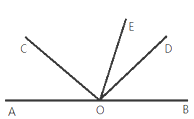
【题目】如图,点A、O、B在同一条直线上,∠AOC=∠BOD,OE是∠BOC的平分线.
(1)若∠AOC=46°,求∠DOE的度数;
(2)若∠DOE=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由. 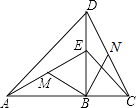
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲从
两地,甲从![]() 地去
地去![]() 地,乙从
地,乙从![]() 地去
地去![]() 地然后立即原路返回
地然后立即原路返回![]() 地,返回时的速度是原来的2倍,如图是甲、乙两人离
地,返回时的速度是原来的2倍,如图是甲、乙两人离![]() 地的距离
地的距离![]() (千米)和时间
(千米)和时间![]() (小时)之间的函数图象.
(小时)之间的函数图象.
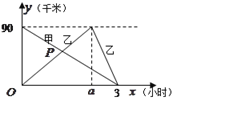
请根据图象回答下列问题:
(1)![]() 、
、![]() 两地的距离是 千米,
两地的距离是 千米, ![]() ;
;
(2)求![]() 的坐标,并解释它的实际意义;
的坐标,并解释它的实际意义;
(3)请直接写出当![]() 取何值时,甲乙两人相距15千米.
取何值时,甲乙两人相距15千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=![]() ,直接写出∠DOE的度数(用含
,直接写出∠DOE的度数(用含![]() 的代数式表示);
的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
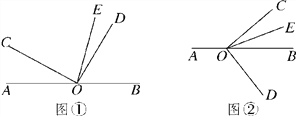
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三连个月投放单车数量的月平均增长率为x,则所列方程正确的是( )
A.1000(1+x)2=440B.1000(1+x)2=1000
C.1000(1+2x)=1000+440D.1000(1+x)2=1000+440
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com