
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由. 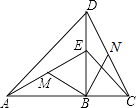
【答案】解:BM=BN,BM⊥BN,
理由是:在△ABE和△DBC中,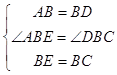 ,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,
∴∠ABD=∠DBC=90°,
∵M为AE的中点,N为CD的中点,
∴BM=AM=EM= ![]() AE,BN=CN=DN=
AE,BN=CN=DN= ![]() CD,
CD,
∴BM=BN,∠EAB=∠MBA,∠CDB=∠DBN,∠AEB=∠EBM,∠NCB=∠NBC,
∵∠EAB=∠BDC,∠AEB=∠DCB,
∴∠ABM=∠DBN,∠EBM=∠NBC,
∴∠ABC=2∠DBN+2∠EBM=180°,
∴∠EBN+∠EBM=90°,
∴BM⊥BN.
【解析】根据SAS推出△ABE≌△DBC,推出AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,求出∠ABD=∠DBC=90°,BM=AM=EM= ![]() AE,BN=CN=DN=
AE,BN=CN=DN= ![]() CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
【考点精析】本题主要考查了直角三角形斜边上的中线的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】一家商场将某种型号的彩电按物价部门核准的最高售价提高30%,然后标出”“大酬宾,八折优惠,经顾客投诉后,执法部门按所得的非法收入的10倍处以每台1000元的罚款,则每台的彩电按物价部门核准的最高售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是确定事件的是
A. 我校同学中间出现一位数学家
B. 从一副扑克牌中抽出一张,恰好是大王
C. 从装着九个红球、一个白球共十个球的袋中任意摸出两个,其中一定有红球
D. 未来十年内,印度洋地区不会发生海啸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列推证过程补充完整. 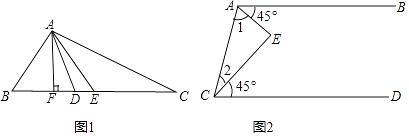
(1)如图1,在△ABC中,AE是中线,AD是角平分线,AF是高.
①BE== ![]() ;
;
②∠BAD== ![]() ;
;
③∠AFB==90°;
④S△ABC= .
(2)如图2,AB∥CD,∠BAE=∠DCE=45°,
∵AB∥CD
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于O.OF是∠BOD的平分线,OE⊥OF.
(1)若∠BOE比∠DOF大38°,求∠DOF和∠AOC的度数;
(2)试问∠COE与∠BOE之间有怎样的大小关系?请说明理由.
(3)∠BOE的余角是 ,∠BOE的补角是 .
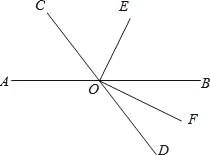
查看答案和解析>>
科目:初中数学 来源: 题型:
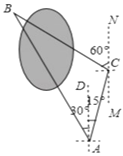
【题目】小明同学要测量公园内被湖水隔开的两颗大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°的方向.
(1)求∠ABC的度数;
(2)求两棵大树A和B之间的距离(结果精确到1米;参考数据![]() ,
, ![]() ,
, ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com