
【题目】在我市双城同创的工作中,某社区计划对1200m2的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为300m2区域的绿化时,甲队比乙队少用3天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数关系式.
(3)若甲队每天绿化费用为0.4万元,乙队每天绿化费用为0.15万元,且甲、乙两队施工的总天数不超过14天,则如何安排甲、乙两队施工的天数,使施工费用最少?并求出最少费用.
【答案】
(1)解:设乙工程队每天能完成绿化的面积是xm2,
根据题意得: ![]() ﹣
﹣ ![]() =3,
=3,
解得:x=50,
经检验,x=50是原方程的解,
则甲工程队每天能完成绿化的面积是50×2=100(m2),
答:甲、乙两工程队每天能完成的面积分别是100m2、50m2;
(2)解:由题意得:100x+50y=1200,
整理得:y= ![]() =24﹣2x;
=24﹣2x;
(3)解:设应甲队的工作a天,则乙队工作b天,(0≤a≤14,0≤b≤14)
根据题意得,100a+50b=1200,
∴b=24﹣2a
a+b≤14,
∴a+24﹣2a≤14,
∴a≥10
w=0.4a+0.15b=0.4a+0.15(24﹣2a)=0.1a+3.6,
∴当a=10时,W最少=0.1×10+3.6=4.6万元.
【解析】(1)设乙工程队每天能完成绿化的面积是xm2 , 根据在独立完成面积为300m2区域的绿化时,甲队比乙队少用3天,列方程求解;(2)用总工作量减去甲队的工作量,然后除以乙队的工作效率即可求解;(3)设应安排甲队工作a天,乙队的工作天,列不等式组求解.
【考点精析】利用分式方程的应用对题目进行判断即可得到答案,需要熟知列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系. 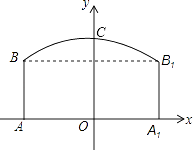
(1)求该抛物线的函数表达式,并求出自变量x的取值范围;
(2)一大型货运汽车装载大型设备后高为6m,宽为4m.如果该隧道内设双向行车道,那么这辆货车能否安全通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号) 根据以上信息,解答下列问题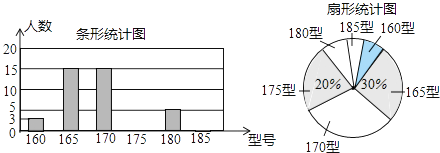
(1)该班共有多少名学生,其中穿175型号校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整;
(3)在扇形统计图中,请计算185型号校服所对应的扇形圆心角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( ) 
A.35°
B.40°
C.50°
D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图; 
(1)这次抽取的学生的人数是;
(2)补全条形统计图;
(3)在扇形统计图中C等级所对应的圆心角为度;
(4)该校九年级学生有1500人,请你估计其中A等级的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE= ![]() ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF . 正确的个数是( )
﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF . 正确的个数是( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ![]() ),B(4,0)两点.
),B(4,0)两点.
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 ![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com