
 ����������������A��B��C�����DZ�ʾ���������ֱ�Ϊa��b��c����֪a�����ĸ���������|b+4|+��c-2��2=0��
����������������A��B��C�����DZ�ʾ���������ֱ�Ϊa��b��c����֪a�����ĸ���������|b+4|+��c-2��2=0������ ��1�������������ĸ������a���ٸ��ݷǸ�����������ʽ���b��c��ֵ��Ȼ��д��A��B��C�����ʾ�������ɣ�
��2�������D��ʾ����Ϊx��Ȼ���ʾ����D����A��C�ľ��벢�г�������⼴�ɣ�
�����E��ʾ����Ϊy��Ȼ���г�����ֵ������⼴�ɣ�
��3�����F��ʾ����Ϊz��Ȼ���г�����ֵ���̣�����⼴�ɣ�
��� �⣺��1����a�����ĸ�������
��a=-1��
������ã�b+4=0��c-2=0��
���b=-4��c=2��
���ԣ���A��B��C��ʾ�����ֱ�Ϊ-1��-4��2��
��2�������D��ʾ����Ϊx��
������ã�x-��-1��=2-x��
���x=$\frac{1}{2}$��
���ԣ���D��ʾ����Ϊ$\frac{1}{2}$��
�����E��ʾ����Ϊy��
������ã�|y-��-1��|=2��
���ԣ�y+1=2��y+1=-2��
���y=1��y=-3��
���ԣ���E��ʾ����Ϊ1��-3��
�ʴ�Ϊ��$\frac{1}{2}$��1��-3��
��3�����F��ʾ����Ϊz��
������ã�|z-��-1��|=2|z-��-4��|��
���ԣ�z+1=2��z+4����z+1=-2��z+4����
���z=-7��z=-3��
���ԣ���F��ʾ����Ϊ-7��-3��
���� ���⿼���˷Ǹ��������ʣ������Ǹ����ĺ�Ϊ0ʱ���⼸���Ǹ�����Ϊ0�������������ľ���ı�ʾ��ȷ�г������ǽ���Ĺؼ���


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
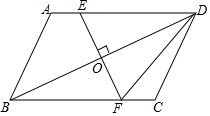 ��֪����ͼ��AD��BC��EF��ֱƽ��BD����AD��BC��BD�ֱ��ڵ�E��F��O����֤��
��֪����ͼ��AD��BC��EF��ֱƽ��BD����AD��BC��BD�ֱ��ڵ�E��F��O����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���߶�AB�����˵������ֱ���A��6��4����B��8��2������ԭ��OΪλ�����ģ��ڵ�һ�����ڽ��߶�AB��СΪԭ����$\frac{1}{2}$��õ��߶�CD����˵�C������Ϊ��3��2����
��ͼ���߶�AB�����˵������ֱ���A��6��4����B��8��2������ԭ��OΪλ�����ģ��ڵ�һ�����ڽ��߶�AB��СΪԭ����$\frac{1}{2}$��õ��߶�CD����˵�C������Ϊ��3��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC��D��E�ǡ�ABC�����㣬ADƽ�֡�BAC����EBC=��E=60�㣬��BE=10cm��DE=2cm����BC=12cm��
��ͼ���ڡ�ABC�У�AB=AC��D��E�ǡ�ABC�����㣬ADƽ�֡�BAC����EBC=��E=60�㣬��BE=10cm��DE=2cm����BC=12cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com