
分析 (1)根据题意可以分别用代数式表示出在甲、乙两城市乘坐出租车x(x>3)千米各自的收费;
(2)将x=8分别代入(1)中的两个代数式,从而可以解答本题.
解答 解:(1)在甲城市乘坐出租车x千米应收费:7+(x-3)×1.7=7+1.7x-5.1=(1.7x+1.9)元,
在乙城市乘坐出租车x千米应收费:10+(x-3)×1.2=10+1.2x-3.6=(1.2x+6.4)元,
即在甲城市乘坐出租车x(x>3)千米收费为:(1.7x+1.9)元,在乙城市乘坐出租车x(x>3)千米收费为:(1.2x+6.4)元;
(2)解:当x=8时,
1.7x+1.9=1.7×8+1.9=15.5(元),1.2x+6.4=1.2×8+6.4=16(元),
∵16-15.5=0.5,
∴在甲、乙两城市乘坐出租车的路程都为8千米,乙城市的收费高些,高0.5元.
点评 本题考查列代数式,解题的关键是明确题意,列出相应的代数式.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
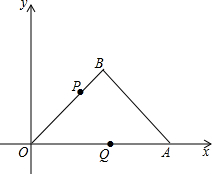 如图,∠OAB=45°,点A的坐标是(4,0),AB=$2\sqrt{2}$,连结OB.
如图,∠OAB=45°,点A的坐标是(4,0),AB=$2\sqrt{2}$,连结OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
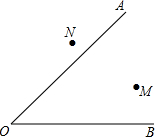 已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法).
已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+$\frac{1}{{x}^{2}}$=1 | B. | (x-1)(x+2)=1 | C. | ax2+bx+c=0 | D. | 3x2-5xy-5y2=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com