
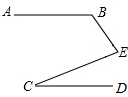
 如图所示,AB∥CD,若∠B=120°,∠C=35°,则∠E=95°.
如图所示,AB∥CD,若∠B=120°,∠C=35°,则∠E=95°.  黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
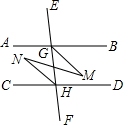 如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.
如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
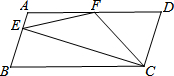 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
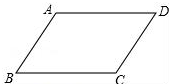 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
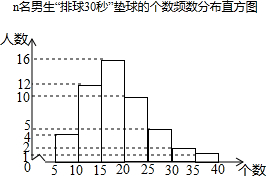 某校为了预测九年级男生“排球30秒”对墙垫球的情况,从本校九年级随机抽取了n名男生进行该项目测试,并绘制出如下的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题:
某校为了预测九年级男生“排球30秒”对墙垫球的情况,从本校九年级随机抽取了n名男生进行该项目测试,并绘制出如下的频数分布直方图,其中从左到右依次分为七个组(每组含最小值,不含最大值).根据统计图提供的信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com