
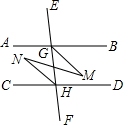
 如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.
如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.分析 (1)由∠EGB、∠EHD均与∠CHE互补可得出∠EGB=∠EHD,由同旁内角相等两直线平行即可得出结论;
(2)由AB∥CD可得出∠BGF=∠CHE,由角平分线的定义可得出∠NHE=∠MGF,由内错角相等两直线平行得出GM∥NH,从而得出∠M=∠N;
(3)由角平分线的定义可得出∠BGF=2∠MGB,结合给定的比例关系与∠EGB、∠BGH互补可算出∠BGF的度数,再根据(2)的结论即可得出∠CHN的度数.
解答 (1)证明:∵∠EGB+∠CHE=180°,∠CHE+∠EHD=180°,
∴∠EGB=∠EHD,
∴AB∥CD.
(2)证明:∵AB∥CD,
∴∠BGF=∠CHE,
∵GM平分∠BGF,HN平分∠CHE,
∴∠NHE=∠MGF,
∴GM∥NH,
∴∠M=∠N.
(3)解:∵GM平分∠BGF,
∴∠BGF=2∠MGB,
又∵∠EGB:∠MGB=5:2,且∠EGB+∠BGF=180°,
∴∠BGF=$\frac{2×2}{5+2×2}$×180°=80°,
∴∠MGB=40°,
∵∠CHN=∠NHE=∠MGF=∠MGB,
∴∠CHN=40°.
点评 本题考查了平行线的判定与性质以及角的计算,解题的关键是:(1)根据角的关系找出相等的同旁内角;(2)根据角的关系找出相等的内错角证平行;(3)根据比例和角平分线的定义算出∠BGF的度数.本题属于基础题,难度不大,解决该题型题目时,根据角与角之间的关系寻找相等或者互补的角来证平行.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 每个小长方形的面积等于频数 | B. | 每个小长方形的面积等于频率 | ||
| C. | 频率=$\frac{频数}{数据总数}$ | D. | 各个小长方形面积和等于1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
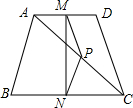 如图,在四边形ABCD中,AB=DC,P是对角线AC的中点,M是AD的中点,N是BC的中点.
如图,在四边形ABCD中,AB=DC,P是对角线AC的中点,M是AD的中点,N是BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
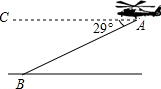 一架直升机到某失事地点进行搜救,直升机飞到A处时,探测前方地面上B处有一生命体,从A处观测B处的俯角为29°,该直升机一直保持在距地面100米高度直线飞行搜索,飞行速度为10米/秒,求该直升机从A处飞到生命体的正上方时所用的时间.(结果精确到0.1秒)
一架直升机到某失事地点进行搜救,直升机飞到A处时,探测前方地面上B处有一生命体,从A处观测B处的俯角为29°,该直升机一直保持在距地面100米高度直线飞行搜索,飞行速度为10米/秒,求该直升机从A处飞到生命体的正上方时所用的时间.(结果精确到0.1秒)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com