
分析 (1)由②变形得:3(3x-2y)+2y=19③,把①代入③得:15+2y=19,即y=2即可;
(2)由②变形化简得x2+4y2=18-$\frac{xy}{2}$③,整体代入即可.
解答 解:(1)由②变形得:3(3x-2y)+2y=19③,
把①代入③得:15+2y=19,即y=2,
把y=2代入①得:x=3,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$;
(2)由②变形得:2(x2+4y2)+xy=36,即:x2+4y2=18-$\frac{xy}{2}$③,
由①变形得:3(x2+4y2)-2xy=47④,
把③代入④得:3×(18-$\frac{xy}{2}$)-2xy=47,
∴xy=2.
点评 此题考查了解二元一次方程组,熟练掌握整体代入是解本题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
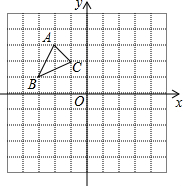 如图,△ABC的顶点分别为:A(-2,3),B(-3,1),C(-1,2).
如图,△ABC的顶点分别为:A(-2,3),B(-3,1),C(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{1000}$ | B. | $\frac{1}{500}$ | C. | $\frac{1}{200}$ | D. | $\frac{95}{1000}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
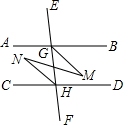 如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.
如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
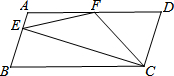 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com