
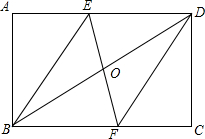
 如图所示,将矩形ABCD沿EF对折,使点B与点D重合,折痕为EF,请判断四边形BFDE的形状,并证明你的结论.
如图所示,将矩形ABCD沿EF对折,使点B与点D重合,折痕为EF,请判断四边形BFDE的形状,并证明你的结论. 分析 先根据折叠的性质得出OB=OD,BF=FD.再由ASA证明△DOE≌△BOF,得出OE=OF,根据对角线互相平分的四边形是平行四边形证出四边形BFDE为平行四边形,进而根据有一组邻边相等的平行四边形是菱形得出四边形BFDE是菱形.
解答 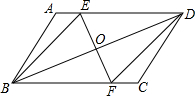 解:四边形BFDE是菱形.理由如下:
解:四边形BFDE是菱形.理由如下:
∵把平行四边形ABCD翻折,使B点与D点重合,EF为折痕,
∴OB=OD,BF=FD.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OBF=∠ODE.
在△DOE和△BOF中,
$\left\{\begin{array}{l}{∠ODE=∠OBF}\\{OD=OB}\\{∠DOE=∠BOF}\end{array}\right.$,
∴△DOE≌△BOF,
∴OE=OF,
又∵OB=OD,
∴四边形BFDE为平行四边形,
又∵BF=FD,
∴四边形BFDE是菱形.
点评 本题考查了轴对称的性质,全等三角形的判定与性质,平行四边形的判定与性质,菱形的判定,综合性较强,难度中等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
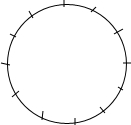 八年级(3)班48人参加课外活动,有16人打篮球,8人打乒乓球,4人跳绳,12人打排球,其余人参加长跑,请在如图的十二等分的圆周上,用扇形统计图表示学生参加课外活动的情况.
八年级(3)班48人参加课外活动,有16人打篮球,8人打乒乓球,4人跳绳,12人打排球,其余人参加长跑,请在如图的十二等分的圆周上,用扇形统计图表示学生参加课外活动的情况.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
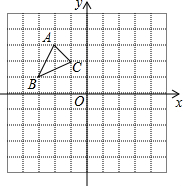 如图,△ABC的顶点分别为:A(-2,3),B(-3,1),C(-1,2).
如图,△ABC的顶点分别为:A(-2,3),B(-3,1),C(-1,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
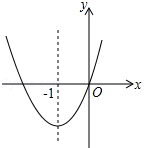 如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线y=ax2+bx+c,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0.正确的个数是( )
如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线y=ax2+bx+c,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0.正确的个数是( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
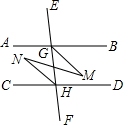 如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.
如图,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
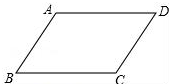 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com