
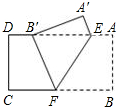
 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,∠EFB=60°,则四边形A′B′FE的周长是=17.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,∠EFB=60°,则四边形A′B′FE的周长是=17. 分析 根据折叠的性质得出A'B'=AB=4,A′E=AE=3,∠A′=∠A=90°,在直角△A'B'E中,利用勾股定理求出B'E=$\sqrt{A′B{′}^{2}+A′{E}^{2}}$=5.再根据折叠的性质以及平行线的性质证明∠B'FE=∠B'EF=60°,那么△B'EF是等边三角形,从而得出B'F=EF=B'E=5,然后根据四边形的周长公式计算即可.
解答 解:∵把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,
∴A'B'=AB=4,A′E=AE=3,∠A′=∠A=90°.
∵直角△A'B'E中,A'B'=4,A′E=3,∠A′=90°,
∴B'E=$\sqrt{A′B{′}^{2}+A′{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
∵矩形ABCD中,AD∥BC,
∴∠B'EF=∠EFB=60°,
又∵∠B'FE=∠EFB=60°,
∴∠B'FE=∠B'EF=60°,
∴△B'EF是等边三角形,
∴B'F=EF=B'E=5,
∴四边形A′B′FE的周长=A′B′+B′F+EF+AE′=4+5+5+3=17.
故答案为17.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理,矩形的性质,等边三角形的判定与性质,求出B'F=EF=B'E=5是解题的关键.


 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
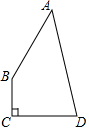 四边形ABCD中,AB=12,BC=3,CD=4,AD=13,且∠C=90°,则四边形ABCD的面积为( )
四边形ABCD中,AB=12,BC=3,CD=4,AD=13,且∠C=90°,则四边形ABCD的面积为( )| A. | 84 | B. | 36 | C. | 54 | D. | 72 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
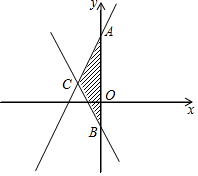 已知直线y=2x+3与直线y=-2x-1.
已知直线y=2x+3与直线y=-2x-1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
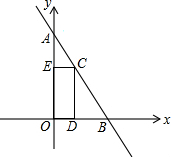 如图,一次函数y=-x+2的图象与两坐标轴分别交于A、B两点,点C是线段AB上一动点,过点C分别作CD、CE垂直于x轴、y轴于点D、E,当点C从点A出发向点B运动时(不与点B重合),矩形CDOE的周长( )
如图,一次函数y=-x+2的图象与两坐标轴分别交于A、B两点,点C是线段AB上一动点,过点C分别作CD、CE垂直于x轴、y轴于点D、E,当点C从点A出发向点B运动时(不与点B重合),矩形CDOE的周长( )| A. | 逐渐变大 | B. | 不变 | C. | 逐渐变小 | D. | 先变小后变大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
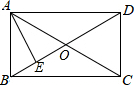 如图,矩形ABCD的对角线交于点O,∠AOB=36°,AE平分∠BAC交BD于点E,若AC=4,则AB的长度为( )
如图,矩形ABCD的对角线交于点O,∠AOB=36°,AE平分∠BAC交BD于点E,若AC=4,则AB的长度为( )| A. | $\sqrt{5}$-2 | B. | 5-$\sqrt{5}$ | C. | $\sqrt{5}$-1 | D. | 4-$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )
如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )| A. | 50 | B. | 45 | C. | 40 | D. | 35 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 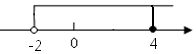 | B. | 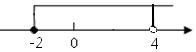 | ||
| C. | 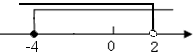 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
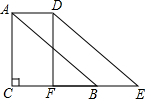 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿着水平方向向右平移后得到△DEF,若F为BC的中点,则四边形ABED的面积为( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿着水平方向向右平移后得到△DEF,若F为BC的中点,则四边形ABED的面积为( )| A. | 12 | B. | 24 | C. | 48 | D. | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 分组/cm | 频 数 | 频 率 |
| 145~150 | 2 | 0.05 |
| 150~155 | a | 0.15 |
| 155~160 | 14 | 0.35 |
| 160~165 | b | c |
| 165~170 | 6 | 0.15 |
| 合计 | 40 | 1.00 |
| A. | 6,12,0.30 | B. | 6,10,0.25 | C. | 8,12,0.30 | D. | 6,12,0.24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com