
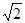 ≈1.41,
≈1.41, ≈1.73,
≈1.73,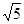 ≈2.24,
≈2.24, ≈2.45)
≈2.45)
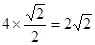 …………2分
…………2分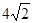 ≈
≈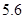
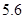 米. …………………………………… 4分
米. …………………………………… 4分 
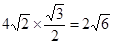 ……………6分
……………6分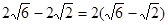 ≈2.1
≈2.1 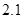 米.………………………………8分
米.………………………………8分

 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源:不详 题型:填空题
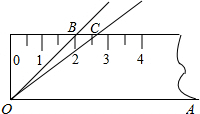
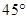 的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将
的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将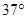 的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm
的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm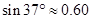 ,
,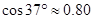 ,
,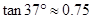 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
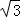 )、D(0,3
)、D(0,3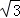 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.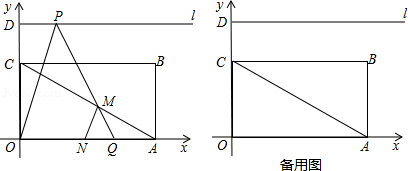
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
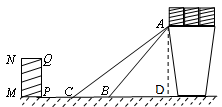
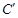 处,得折痕EF;
处,得折痕EF;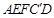 折叠,使AE、
折叠,使AE、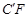 重合,得折痕DG,再打开;
重合,得折痕DG,再打开;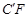 均落在DG上,点A、
均落在DG上,点A、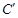 落在点
落在点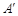 处,点E、F落在点
处,点E、F落在点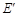 处,得折痕MN、QP.这样,就可以折出一个五边形DMNPQ.
处,得折痕MN、QP.这样,就可以折出一个五边形DMNPQ.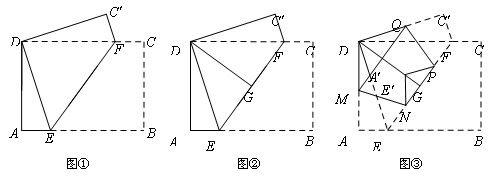
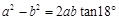 ; ②
; ②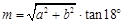 ;
;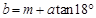 ; ④
; ④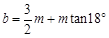 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com