
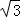 )、D(0,3
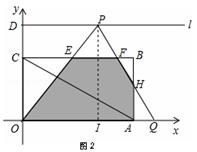
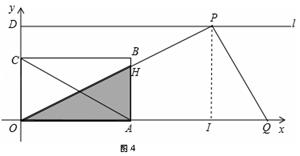
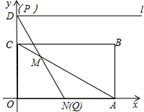
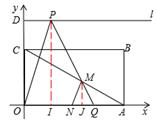
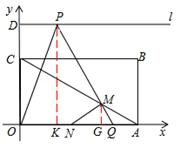
)、D(0,3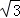 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.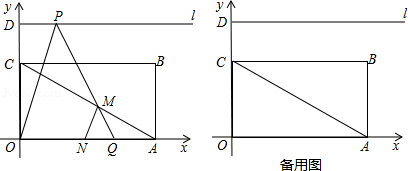
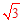 )。 ②30。③(3,3
)。 ②30。③(3,3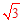 )。
)。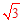 或m=2。
或m=2。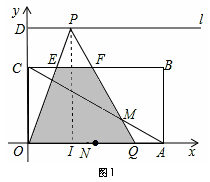
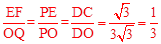 ,∴EF=
,∴EF= (3+x),
(3+x),
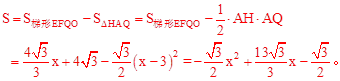
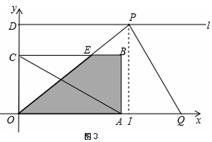
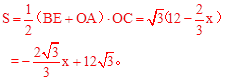
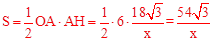 。
。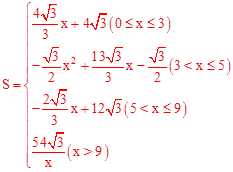 。
。 ),∴点B的坐标为:(6,2
),∴点B的坐标为:(6,2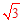 )。
)。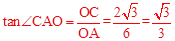 ,∴∠CAO=30°。
,∴∠CAO=30°。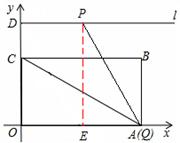
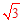 ),∴PE=3
),∴PE=3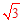 。
。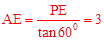 。
。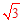 )。
)。

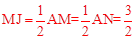 ,
,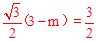 ,解得:m=3﹣
,解得:m=3﹣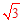 。
。
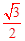 。
。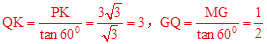 。
。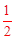 AN=1.5。∴OK=2。∴m=2。
AN=1.5。∴OK=2。∴m=2。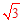 或m=2。
或m=2。

科目:初中数学 来源:不详 题型:解答题
 取1.73).
取1.73).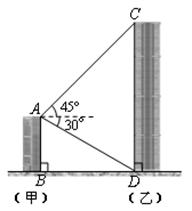
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,若cos
,若cos =
=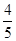 ,OC =" 15" ,求AB的长。
,OC =" 15" ,求AB的长。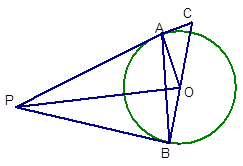
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
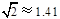 ,
,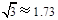 )
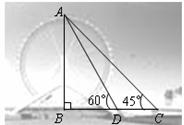
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
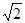 ≈1.41,
≈1.41, ≈1.73,
≈1.73,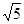 ≈2.24,
≈2.24, ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
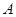 处运往正东方向的
处运往正东方向的 处,在点
处,在点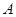 处测得某岛
处测得某岛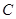 在北偏东
在北偏东 的方向上.该货船航行
的方向上.该货船航行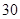 分钟后到达
分钟后到达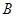 处,此时再测得该岛在北偏东
处,此时再测得该岛在北偏东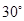 的方向上,已知在
的方向上,已知在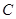 岛周围
岛周围 海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.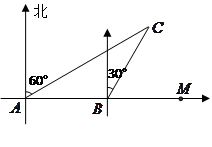
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com