
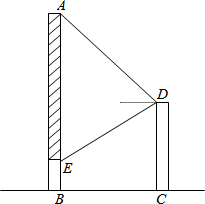
 开业庆典,在甲建筑物上从A点到E点持一宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,甲乙两建筑物之间的水平距离BC为40米,这条宣传条幅AE的长(精确到0.01米).
开业庆典,在甲建筑物上从A点到E点持一宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,甲乙两建筑物之间的水平距离BC为40米,这条宣传条幅AE的长(精确到0.01米). 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
| A、3.01×103 |
| B、3.01×105 |
| C、3.0067×105 |
| D、30.1×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:
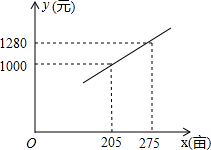 国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,计划明年再承租不超过90亩的土地种粮以增加收入,考虑各种因素,政府预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示:
国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,计划明年再承租不超过90亩的土地种粮以增加收入,考虑各种因素,政府预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com