
【题目】如图,正六边形ABCDEF的边长为2![]() cm,点P为六边形内任一点.则点P到各边距离之和为_____cm.
cm,点P为六边形内任一点.则点P到各边距离之和为_____cm.
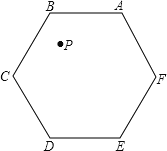
【答案】18.
【解析】
过P作AB的垂线,交AB、DE分别为H、K,连接BD,由正六边形的性质可知AB∥DE,AF∥CD,BC∥EF,故HK⊥DE,过C作CG⊥BD,由等腰三角形的性质及正六边形的内角和定理可知,DB⊥AB⊥DE,再由锐角三角函数的定义可求出BG的长,进而可求出BD的长,由正六边形的性质可知点P到AF与CD的距离和及P到EF、BC的距离和均为BD的长.
如图所示:过P作AB的垂线,交AB、DE分别为H、K,连接BD,
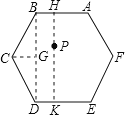
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK,
∵CG⊥BD,
∴BD=2BG=2×BC×cos∠CBD=2×2![]() ×
×![]() =6,
=6,
∴点P到各边距离之和为3BD=3×6=18.
故答案是:18.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
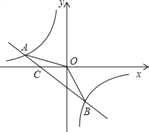
【题目】如图,已知A(–4,n),B(2,–4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式![]() 的解集(请直接写出答案).
的解集(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰![]() 中,
中,![]() ,
,![]() 的顶点
的顶点![]() 在线段
在线段![]() 上,不与
上,不与![]() 重合.
重合.
(1)如图①,若![]() 且点
且点![]() 在
在![]() 中点时,四边形
中点时,四边形![]() 是什么四边形并证明?
是什么四边形并证明?
(2)将![]() 绕点
绕点![]() 旋转至如图②所示位置,若
旋转至如图②所示位置,若![]() ,设
,设![]() 的面积为
的面积为![]() ;
;![]() 的面积为
的面积为![]() ,求
,求![]() 的值(用含有
的值(用含有![]() 的代数式表示).
的代数式表示).
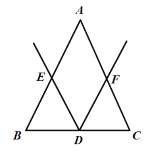
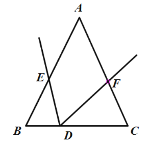
图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题:
(1)该超市“元旦”期间共销售 个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度;
(2)补全条形统计图;
(3)如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距![]() (米),甲行走的时间为
(米),甲行走的时间为![]() (分),
(分),![]() 关于
关于![]() 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画![]() 关于
关于![]() 函数图象的其余部分;
函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
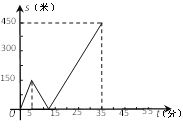
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() .对角线
.对角线![]() 相交于点
相交于点![]() ,反比例函数
,反比例函数![]() 的图像经过点
的图像经过点![]() ,分别与
,分别与![]() 交于点
交于点![]() .
.
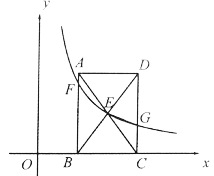
(1)若![]() ,求
,求![]() 的值;
的值;
(2)连接![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
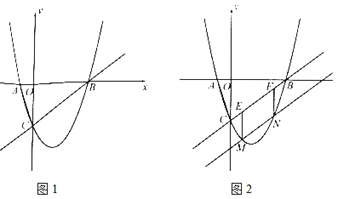
(1)求二次函数的表达式及点![]() 、点
、点![]() 的坐标;
的坐标;
(2)若点![]() 在二次函数图像上,且
在二次函数图像上,且![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(3)将直线![]() 向下平移,与二次函数图像交于
向下平移,与二次函数图像交于![]() 两点(
两点(![]() 在
在![]() 左侧),如图2,过
左侧),如图2,过![]() 作
作![]() 轴,与直线
轴,与直线![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() 轴,与直线
轴,与直线![]() 交于点
交于点![]() ,当
,当![]() 的值最大时,求点
的值最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,BC=4,∠ABC=60°,BD平分∠ABC,交AC于点D,M,N分别是BD,BC上的动点,则CM+MN的最小值是( )

A. ![]() B. 2C. 2
B. 2C. 2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四张完全相同的不透明卡片,其正面分别写有数字-2,-1,0,2,把这四张卡片背面朝上洗匀后放在桌面上.
(1)随机抽取一张卡片,求抽取的卡片上的数字为负数的概率;
(2)先随机抽取卡片,其上的数字作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线y=2x上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com