Question

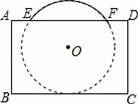
把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为　　　　　　．

Answer 1

　5　．

【考点】垂径定理的应用；勾股定理；切线的性质．

【专题】几何图形问题．

【分析】首先由题意，⊙O与BC相切，记切点为G，作直线OG，分别交AD、劣弧于点H、I，再连接OF，易求得FH的长，然后设求半径为r，则OH=8﹣r，然后在Rt△OFH中，r²﹣（16﹣r）²=8²，解此方程即可求得答案．

【解答】解：由题意，⊙O与BC相切，记切点为G，作直线OG，分别交AD、劣弧于点H、I，再连接OF，

在矩形ABCD中，AD∥BC，而IG⊥BC，

∴IG⊥AD，

∴在⊙O中，FH=EF=4，

设求半径为r，则OH=8﹣r，

在Rt△OFH中，r²﹣（8﹣r）²=4²，

解得r=5，

故答案为：5．

【点评】此题考查了切线的性质、垂径定理以及勾股定理．此题难度适中，注意掌握辅助线的作法，注意掌握方程思想与数形结合思想的应用．