
如图1,平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,顶点为M.D在y轴上,OB=OD=3,OA=5.
(1)试用含a的式子表示点M的坐标;
(2)若S△ABC﹣S△ACM=
 ;
;
①求抛物线y=ax2+bx+c的解析式;
②如图2,将△BOD绕点O沿逆时针方向旋转α(0°<α≤180°)得到△B′OD′,直线AD与BC相交于点Q,求点Q纵坐标的取值范围.


【考点】二次函数综合题.
【分析】(1)由线段长度,确定点A,B坐标代入y=ax2+bx+c即可用a表示抛物线,运用顶点公式即可求出点M坐标;
(2)①用a表示△ABC与△ACM的面积,根据题意列方程求解即可;
②根据题意分析出:以点O为圆心,以OB为半径作圆,当AD与圆O在第二象限内相切时,Q的纵坐标最大,当AD与圆O在第三象限内相切时,Q的纵坐标最小,
分别求解即可,求解时,先确定切点坐标,求出两条直线解析式,联立直线解方程组求出y的值即可.
【解答】解:(1)由OB=OD=3,OA=5可得,
点A(﹣5,0),B(3,0),D(0,5),
设抛物线的解析式为y=a(x﹣3)×(x+5),
整理得:y=ax2+2ax﹣15a,
所以顶点M(﹣1,﹣16a);
(2)如图1
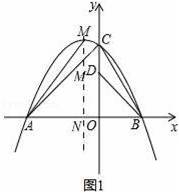

过点M作MN⊥x轴,垂足为N,交直线AC于点H,
y=ax2+2ax﹣15a,令x=0,解得:y=﹣15a,
所以:C(0,﹣15a)
设直线AC解析式为:y=mx+n,
由A(﹣5,0),C(0,﹣15a),坐标可得,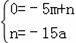
 ,
,
解得: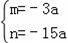
 ,
,
所以直线AC:y=﹣3ax﹣15a,
由M(﹣1,﹣16a),可得,
点H(﹣1,﹣12a),
所以MH=﹣16a﹣(﹣12a)=﹣4a,
所以:S△ACM=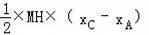
 =
=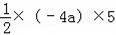
 =﹣10a,
=﹣10a,
S△ABC=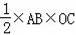
 =﹣60a,
=﹣60a,
由S△ABC﹣S△ACM=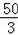
 ,
,
解得:a=﹣
 ,
,
所以:抛物线的解析式为:y=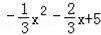
 ;
;
②如图2
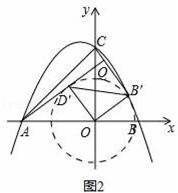

以点O为圆心,以OB为半径作圆,当AD与圆O在第二象限内相切时,Q的纵坐标最大,
此时,易求点D′的坐标为(﹣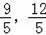
 ),点A(﹣5,0);点B′(
),点A(﹣5,0);点B′(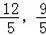
 ),
),
用两点法可求直线AD′解析式为:y=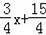
 ,
,
直线B′C的解析式为: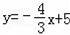
 ,
,
联立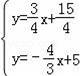
 ,
,
解得y=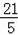
 ,
,
如图3


以点O为圆心,以OB为半径作圆,当AD与圆O在第三象限内相切时,Q的纵坐标最小,
此时易求点D′(
 ,
,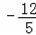
 ),点A(﹣5,0);点B′(﹣
),点A(﹣5,0);点B′(﹣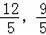
 ),
),
用两点法可求直线AD′解析式为: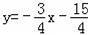
 ,
,
直线B′C的解析式为: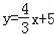
 ,
,
联立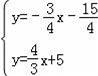
 ,
,
解得:y=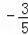
 .
.
所以:点Q纵坐标的取值范围为: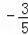
 ≤y≤
≤y≤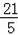
 .
.
【点评】此题主要考查二次函数的综合问题,会用已知点求解析式,会根据点的坐标表示三角形面积,会运用圆的知识分析解决旋转的相关问题是解题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
2016年全国两会在3月3日开幕,引起了传媒的极大关注.某网络平台在3月1日至8日,共检测到两会对于民生问题相关信息约290 000条,数290 000用科学记数法表示为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).


查看答案和解析>>
科目:初中数学 来源: 题型:
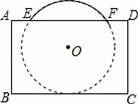
把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3)
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求△PAB的面积.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com