分析:(1)利用同底数幂的乘法法则:底数不变,只把指数相加,即可得到结果;
(2)根据同底数幂的除法法则:底数不变,指数相减,再根据乘方的意义进行化简可得结果;
(3)根据积的乘方运算法则:把积中每一个因式分别乘方,并把结果相乘可得结果;
(4)根据幂的乘方法则:底数不变,指数相乘进行计算,可得结果;
(5)观察多项式的乘法,发现原式为3m与2n之和与之差的积,符合平方差公式的特点,故利用平方差公式及积的乘方法则即可得到结果;
(6)观察原式,发现原式符合完全平方公式的特点,故利用完全平方公式及积的乘方法则可得结果.
解答:解:(1)am•an=am+n;
(2)(-b)3÷(-b)=(-b)3-1=(-b)2=b2;
(3)(-2a)3=(-2)3•a3=-8a3;
(4)(a2)4=a2×4=a8;
(5)(3m+2n)(3m-2n)=(3m)2-(2n)2=9m2-4n2;
(6)(4m-2n)2=(4m)2-2•4m•2n+(2n)2=16m2-16mn+4n2.
故答案为:am+n;b2;-8a3;a8;9m2-4n2;16m2-16mn+4n2
点评:此题考查了整式的混合运算,涉及的运算有同底数幂的乘法,同底数幂的除法,积的乘方,以及幂的乘方,熟练掌握法则是解本题的关键,第五与第六小题主要利用了两个乘法公式,即平方差公式与完全平方公式,要求学生掌握公式的结构特点,利用公式来简化运算.



 教材全解字词句篇系列答案
教材全解字词句篇系列答案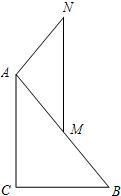 23、如图,在Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.
23、如图,在Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC. 23、如图所示,在△ABE和△ACD中,给出以下4个论断:
23、如图所示,在△ABE和△ACD中,给出以下4个论断: