
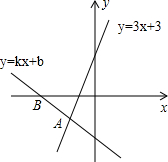 如图,经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),则不等式3x+3<kx+b<0的解集为-3<x<-2.
如图,经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),则不等式3x+3<kx+b<0的解集为-3<x<-2. 分析 由图象得到直线y=kx+b与直线y=4x+2的交点A的坐标(-2,-3)及直线y=kx+b与x轴的交点坐标,观察直线y=3x+3落在直线y=kx+b的下方且直线y=kx+b落在x轴下方的部分对应的x的取值即为所求.
解答 解:∵经过点B(-3,0)的直线y=kx+b与直线y=3x+3相交于点A(-2,-3),
∴直线y=kx+b与直线y=3x+3的交点A的坐标为(-2,-3),直线y=kx+b与x轴的交点坐标为B(-3,0),
又∵当x<-2时,3x+3<kx+b,
当x>-3时,kx+b<0,
∴不等式3x+3<kx+b<0的解集为-3<x<-2.
故答案为-3<x<-2.
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.


科目:初中数学 来源: 题型:填空题
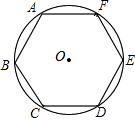 如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.
如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 红球 | B. | 白球 | C. | 黑球 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com