练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．线段AB=10cm，若C点是线段AB的中点，则AC=5cm，CB=5cm．

    分析 根据线段的中点的概念，可得AC=BC=$\frac{1}{2}$AB，代入直接求值即可．

    解答 解：∵AB=10cm，若C点是线段AB的中点，
    ∴AC=CB=$\frac{1}{2}$AB=5cm．
    故答案为：5，5．

    点评 本题考查了两点间的距离，利用中点性质转化线段之间的倍分关系是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    1．如图，正方形A1A2A3A4，A5A6A7A8，A9A10A11A12，…，（每个正方形从第三象限的顶点开始，按顺时针方向顺序，依次记为A1，A2，A3，A4；A5，A6，A7，A8；A9，A10，A11，A12；…）的中心均在坐标原点O，各边均与x轴或y轴平行，若它们的边长依次是2，4，6…，则顶点A2015的坐标为（504，504）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

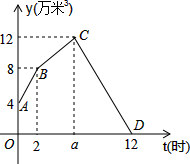    2．某水电站兴建了一个最大蓄水容量为12万米3的蓄水池，并配有2个流量相同的进水口和1个出水口．某天从0时至12时，进行机组试运行．其中，0时至2时打开2个进水口进水；2时，关闭1个进水口减缓进水速度，至蓄水池中水量达到最大蓄水容量后，随即关闭另一个进水口，并打开出水口，直至12时蓄水池中的水放完为止．若这3个水口的水流都是匀速的，水池中的蓄水量y（万米3）与时间t（时）之间的关系如图所示，请根据图象解决下列问题：
    （1）蓄水池中原有蓄水4万米3，蓄水池达最大蓄水量12万米3的时间a的值为6；
    （2）求线段BC、CD所表示的y与t之间的函数关系式；
    （3）蓄水池中蓄水量维持在m万米3以上（含m万米3）的时间有3小时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

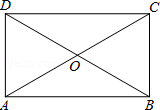    19．如图，在?ABCD中，对角线AC，BD相交于点O，且OA=OB．
    （1）求证：四边形ABCD是矩形；
    （2）若AD=4，∠AOD=50°，求AB的长．（精确到0.1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在矩形纸片ABCD中，AB=16，AD=12，点P在边AB上，若将△DAP沿DP折叠，使点A恰好落在矩形对角线上的点A′处，则AP的长为6或9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．已知?ABCD，边AB=4，AD=8；对角线AC=6，BD=10，则OA=3，BD=5，周长=24．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

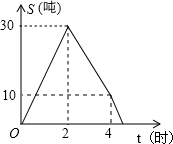    3．某储运部紧急调拨一批物资，连续4小时调进物资，当开始调进物资2小时后又同时开始调出物资，储运部库存物资S（吨）与时间t（小时）之间的函数关系如图所示，下列说法：
    ①调进物资的速度为15吨/小时；
    ②调出物资的速度为25吨/小时；
    ③当调进物资4小时的时候，储运部库存物资为10吨；
    ④这批物资从开始调进到全部调出需要的时间是4.4小时．
    其中正确的个数有（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

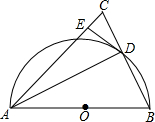    20．如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD．过点D作DE⊥AC，垂足为点E．
    （1）求证：DE是⊙O的切线；
    （2）当⊙O半径为3，CE=2时，求BD长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知：如图，E、F为平行四边形ABCD对角线AC上两点，且AE=CF，连接DE、EB、BF、FD，求证：四边形DEBF为平行四边形．

    查看答案和解析>>

    同步练习册答案