
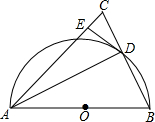
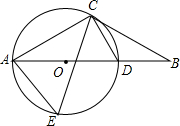
 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.分析 (1)连接OD,AB为⊙0的直径得∠ADB=90°,由AB=AC,根据等腰三角形性质得AD平分BC,即DB=DC,则OD为△ABC的中位线,所以OD∥AC,而DE⊥AC,则OD⊥DE,然后根据切线的判定方法即可得到结论;
(2)由∠B=∠C,∠CED=∠BDA=90°,得出△DEC∽△ADB,得出$\frac{CE}{BD}=\frac{CD}{AB}$,从而求得BD•CD=AB•CE,由BD=CD,即可求得BD2=AB•CE,然后代入数据即可得到结果.
解答 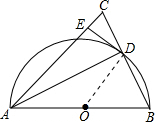 (1)证明:连接OD,如图,
(1)证明:连接OD,如图,
∵AB为⊙0的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分BC,即DB=DC,
∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙0的切线;
(2)证明:∵∠B=∠C,∠CED=∠BDA=90°,
∴△DEC∽△ADB,
∴$\frac{CE}{BD}=\frac{CD}{AB}$,
∴BD•CD=AB•CE,
∵BD=CD,
∴BD2=AB•CE,
∵⊙O半径为3,CE=2,
∴BD=$\sqrt{6×2}$=2$\sqrt{3}$.
点评 本题考查了切线的判定定理:过半径的外端点且与半径垂直的直线为圆的切线.也考查了等腰三角形的性质、三角形相似的判定和性质.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
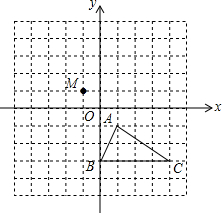 在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).
在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
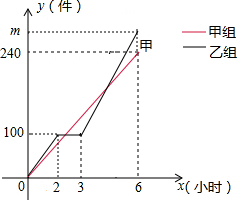 甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )| A. | 甲组加工零件数量y与时间x的关系式为y甲=40x | |
| B. | 乙组加工零件总量m=280 | |
| C. | 经过2$\frac{1}{2}$小时恰好装满第1箱 | |
| D. | 经过4$\frac{3}{4}$小时恰好装满第2箱 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
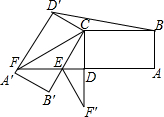 如图在矩形ABCD中,AB=4,将矩形ABCD绕点C顺时针旋转,得到矩形A′B′CD′,AD的延长线分别与B′C、A′D交于点E、F,使CE=2B′E,连接CF,将△CEF沿直线B′C折叠得到△CEF′,当CF′恰好经过点D时,则在△BCD′中以BD′为底的高为$\frac{2\sqrt{21}}{7}$.
如图在矩形ABCD中,AB=4,将矩形ABCD绕点C顺时针旋转,得到矩形A′B′CD′,AD的延长线分别与B′C、A′D交于点E、F,使CE=2B′E,连接CF,将△CEF沿直线B′C折叠得到△CEF′,当CF′恰好经过点D时,则在△BCD′中以BD′为底的高为$\frac{2\sqrt{21}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆.
如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,长方体的底面是边长为1cm的正方形,高为3cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,请利用侧面展开图计算所用细线最短需要多少5cm.
如图,长方体的底面是边长为1cm的正方形,高为3cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,请利用侧面展开图计算所用细线最短需要多少5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com