
【题目】某公园有一座雕塑D,在北门B的正南方向,BD为100米,小树林A在北门的南偏西60°方向,荷花池C在北门B的东南方向,已知A,D,C三点在同一条直线上且BD⊥AC:
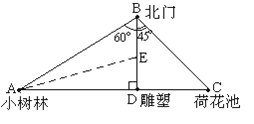
(1)分别求线段AB、BC、AC的长(结果中保留根号,下同);
(2)若有一颗银杏树E恰好位于∠BAD的平分线与BD的交点,求BE的距离.
【答案】(1)、AB=200米;BC=100![]() 米;AC=(100
米;AC=(100![]() +100)米;(2)、BE=(400-200
+100)米;(2)、BE=(400-200![]() )米.
)米.
【解析】
试题分析:(1)、根据Rt△ABD的三角函数得出AB、AD的长度,根据Rt△BCD的三角函数得出BC、DC的长度;(2)、过点E作EF⊥AB,从而得到AF和BF的长度,然后跟BE=2BF得出长度.
试题解析:(1)、AB=200(米),BC=100![]() (米),
(米),
∵AD=100![]() ,DC=100,∴AC=AD+DC=(100
,DC=100,∴AC=AD+DC=(100![]() +100)米
+100)米
(2)、作EF⊥AB,
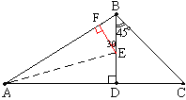
根据角平分线性质,得△AEF≌△AED ∴AF=AD =100![]() 又BE=2BF
又BE=2BF
∴BE=2(AB-AF)=2(200-100![]() )=400-200
)=400-200![]() =(米)
=(米)


科目:初中数学 来源: 题型:
【题目】(10分)九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:

已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p:![]() 和直线l:
和直线l:![]() :
:
(1)对下列命题判断真伪,并说明理由:
①无论k取何实数值,抛物线p总与x轴有两个不同的交点;
②无论k取何实数值,直线l与y轴的负半轴没有交点;
(2)设抛物线p与y轴交点为C,与x轴的交点为A、B,原点O不在线段AB上;直线l与x轴的交点为D,与y轴交点为C1,当OC1=OC+2且OD2=4AB2时,求出抛物线的解析式及最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市为减少雾霾天气采取了多项措施,如对城区主干道进行绿化.现计划把某一段公路的一侧全部栽上银杏树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A. 5(x+21﹣1)=6(x﹣l) B. 5(x+21)=6(x﹣l) C. 5(x+21﹣1)=6x D. 5(x+21)=6x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题共10分)如图,在平面直角坐标系中,![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相切于点
轴相切于点![]() .
.
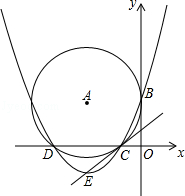
(1)求经过![]() ,
,![]() ,
,![]() 三点的抛物线的函数表达式;
三点的抛物线的函数表达式;
(2)设抛物线的顶点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 相切;
相切;
(3)在![]() 轴下方的抛物线上,是否存在一点
轴下方的抛物线上,是否存在一点![]() ,使
,使![]() 面积最大,最大值是多少?并求出点
面积最大,最大值是多少?并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com