
| A. | 在y轴右侧该抛物线上不存在点M,使S△ACM=3 | |
| B. | 在y轴右侧该抛物线上存在两个点M,使S△ACM=3 | |
| C. | 在y轴右侧该抛物线上存在唯一的点M(2,3),使S△ACM=3 | |
| D. | 在y轴右侧该抛物线上存在唯一的点M(2,-3),使S△ACM=3 |
分析 根据抛物线具有对称性,求出点B的坐标;再根据三角形的面积,求出点C的坐标,根据待定系数法求出抛物线解析式;设在y轴右侧的抛物线上存在点M(m,m2-2m-3),使△ACM的面积为3,根据待定系数法求出直线AM的解析式,确定点N的坐标,根据△AMC的面积求出m的值,从而得解.
解答 解:如图,
由y=ax2-2ax+m可知,对称轴x=$-\frac{b}{2a}=-\frac{-2a}{2a}=1$,
∵点A(-1,0),
∴根据抛物线具有对称性,可得点B(3,0),
∵S△ABC=6,
∴$\frac{1}{2}×4×|y|=6$,解得|y|=3,
∴点C(0,-3),
∴$\left\{\begin{array}{l}{a+2a+m=0}\\{m=-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{m=-3}\end{array}\right.$,
∴抛物线解析式为:y=x2-2x-3,
设在y轴右侧的抛物线上存在点M(m,m2-2m-3),使△ACM的面积为3,
设经过点A,点M的直线AM的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-k+b=0}\\{mk+b={m}^{2}-2m-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=m-3}\\{b=m-3}\end{array}\right.$,
∴直线AM的解析式为:y=(m-3)x+m-3,
∴直线AM与y轴交于点N(0,m-3),
∴${S}_{△ACM}=\frac{1}{2}×(-3-m+3)(m+1)=3$,
解得:m1=-3,m2=2,
∴点M(2,-3),
∴在y轴右侧该抛物线上存在唯一的点M(2,-3),使使△ACM的面积为3.
故选:D.
点评 本题主要考查抛物线与x轴的交点、待定系数法求解析式,设点M的坐标,用含m的式子表示点M的坐标,确定直线解析式,利用分割法求三角形的面积是解决此题的关键,根据题意画出图形,利用数形结合思想解决此题更简单.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
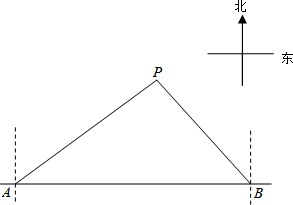 马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | -3 | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
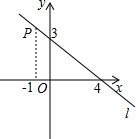 如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;
如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知?ABCD的周长为16cm,AE平分∠BAD交BC于E,设AB=xcm(0<x<4).
如图,已知?ABCD的周长为16cm,AE平分∠BAD交BC于E,设AB=xcm(0<x<4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com