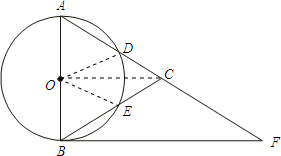
(1)证明:如图,∵∠CBF=∠CFB,
∴CB=CF.
又∵AC=CF,
∴CB=

AF,
∴△ABF是直角三角形,
∴∠ABF=90°,即AB⊥BF.
又∵AB是直径,
∴直线BF是⊙O的切线.
(2)解:如图,连接DO,EO,
∵点D,点E分别是弧AB的三等分点,
∴∠AOD=60°.
又∵OA=OD,
∴△AOD是等边三角形,
∴OA=AD=OD=5,∠OAD=60°,
∴AB=10.
∴在Rt△ABF中,∠ABF=90°,BF=AB•tan60°=10

,即BF=10

;
(3)如图,连接OC.则OC是Rt△ABF的中位线,
∵由(2)知,BF=10

,
∴圆心距OC=

,
∵⊙O半径OA=5.
∴
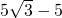
<r<

.
故填:
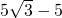
<r<

.
分析:(1)欲证明直线BF是⊙O的切线,只需证明AB⊥BF;
(2)根据圆心角、弧、弦间的关系,等边三角形的判定证得△AOD是等边三角形,所以在Rt△ABF中,∠ABF=90°,∠OAD=60°,AB=10,则利于∠A的正切三角函数的定义来求BF边的长度;
(3)根据已知条件知⊙O与⊙C相交.
点评:本题综合考查了圆心角、弧、弦间的关系,切线的判定与性质,相交两圆的性质,直角三角形的判定与性质以及特殊角的三角函数值等知识点.切线判定定理中所阐述的由位置来判定直线是圆的切线的两大要素:一是经过半径外端;二是直线垂直于这条半径;学生开始时掌握不好并极容易忽视.

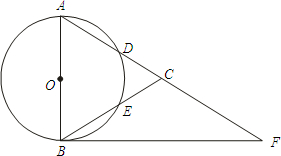 如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB. (1)证明:如图,∵∠CBF=∠CFB,
(1)证明:如图,∵∠CBF=∠CFB, AF,
AF, ,即BF=10
,即BF=10 ;
; ,
, ,
,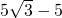 <r<
<r< .
.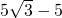 <r<
<r< .
.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为