
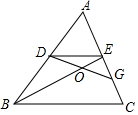
 如图,在△ABC中,点D,E分别是边AB,AC的中点,点G是EC的中点,连接DG交BE于点O,若△ADE的面积为S,求四边形BDGC的面积.
如图,在△ABC中,点D,E分别是边AB,AC的中点,点G是EC的中点,连接DG交BE于点O,若△ADE的面积为S,求四边形BDGC的面积. 分析 由中位线定理得出DE∥BC且$\frac{DE}{BC}$=$\frac{1}{2}$,从而证△ADE∽△ABC得$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=$\frac{1}{4}$,即可知S△ABC=4S,继而得S四边形BDCE=S△ABC-S△ADE=3S,DF⊥AE于点F,由中点定义得出EG=$\frac{1}{2}$EC=$\frac{1}{2}$AE,继而由$\frac{{S}_{△DEG}}{{S}_{△DEA}}$=$\frac{\frac{1}{2}EG•DF}{\frac{1}{2}AE•DF}$=$\frac{EG}{AE}$=$\frac{1}{2}$得S△DEG=$\frac{1}{2}$S,最后由S四边形BDGC=S四边形BDCE-S△DEG得出答案.
解答 解:∵点D,E分别是边AB,AC的中点,
∴DE∥BC,且$\frac{DE}{BC}$=$\frac{1}{2}$,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=$\frac{1}{4}$,
∵S△ADE=S,
∴S△ABC=4S,
则S四边形BDCE=S△ABC-S△ADE=3S,
如图,过点D作DF⊥AE于点F,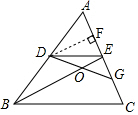
∵点G是EC的中点,且AE=EC,
∴EG=$\frac{1}{2}$EC=$\frac{1}{2}$AE,
则$\frac{{S}_{△DEG}}{{S}_{△DEA}}$=$\frac{\frac{1}{2}EG•DF}{\frac{1}{2}AE•DF}$=$\frac{EG}{AE}$=$\frac{1}{2}$,
∴S△DEG=$\frac{1}{2}$S,
∴S四边形BDGC=S四边形BDCE-S△DEG=3S-$\frac{1}{2}$S=$\frac{5}{2}$S.
点评 本题主要考查相似三角形的判定与性质、中位线定理、三角形的面积及割补法求不规则图形的面积,熟练掌握相似三角形的判定与性质及共高的两三角形的面积比等于底边的比是解题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
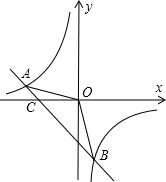 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13cm,12cm,20cm | B. | 8cm,7cm,15cm | C. | 5cm,5cm,11cm | D. | 3cm,4cm,8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{2}{675}$ | B. | $\frac{4}{675}$ | C. | $\frac{2}{675}$或-$\frac{2}{675}$ | D. | $\frac{2}{675}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
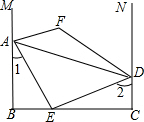 如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )
如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )| A. | 120° | B. | 135° | C. | 150° | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com