
【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.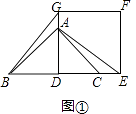
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)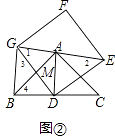
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求 ![]() 的值.
的值.
【答案】
(1)
证明:如图①,
∵AD为等腰直角△ABC的高,
∴AD=BD,
∵四边形DEFG为正方形,
∴∠GDE=90°,DG=DE,
在△BDG和△ADE中
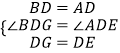 ,
,
∴△BDG≌△ADE,
∴BG=AE
(2)
①证明:如图②,
∵四边形DEFG为正方形,
∴△DEG为等腰直角三角形,
∴∠1=∠2=45°,
由(1)得△BDG≌△ADE,
∴∠3=∠2=45°,
∴∠1+∠3=45°+45°=90°,即∠BGE=90°,
∴BG⊥GE;
②解:设AG=3x,则AE=4x,即GE=7x,
∴DG= ![]() GE=
GE= ![]() x,
x,
∵△BDG≌△ADE,
∴BG=AE=4x,
在Rt△BGA中,AB= ![]() =
= ![]() =5x,
=5x,
∵△ABD为等腰直角三角形,
∴∠4=45°,BD= ![]() AB=
AB= ![]() x,
x,
∴∠3=∠4,
而∠BDM=∠GDB,
∴△DBM∽△DGB,
∴BD:DG=DM:BD,即 ![]() x:
x: ![]() x=DM:
x=DM: ![]() x,解得DM=
x,解得DM= ![]() x,
x,
∴GM=DG﹣DM= ![]() x﹣
x﹣ ![]() x=
x= ![]() x,
x,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1.)如图①,根据等腰直角三角形的性质得AD=BD,再根据正方形的性质得∠GDE=90°,DG=DE,则可根据“SAS“判断△BDG≌△ADE,于是得到BG=AE;
(2.)①如图②,先判断△DEG为等腰直角三角形得到∠1=∠2=45°,再由△BDG≌△ADE得到∠3=∠2=45°,则可得∠BGE=90°,所以BG⊥GE;
②设AG=3x,则AE=4x,即GE=7x,利用等腰直角三角形的性质得DG= ![]() GE=
GE= ![]() x,由(1)的结论得BG=AE=4x,则根据勾股定理得AB=5x,接着由△ABD为等腰直角三角形得到∠4=45°,BD=
x,由(1)的结论得BG=AE=4x,则根据勾股定理得AB=5x,接着由△ABD为等腰直角三角形得到∠4=45°,BD= ![]() AB=
AB= ![]() x,然后证明△DBM∽△DGB,则利用相似比可计算出DM=
x,然后证明△DBM∽△DGB,则利用相似比可计算出DM= ![]() x,所以GM=
x,所以GM= ![]() x,于是可计算出
x,于是可计算出 ![]() 的值.
的值.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.

(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)请在如图所示的网格平面内作出平面直角坐标系,使点A坐标为(1,3)点B坐标为(2,1);
(2)请作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标;
(3)判断△ABC的形状.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
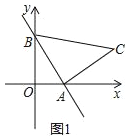
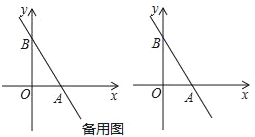
【题目】一次函数y=﹣2x+2的图象与x轴、y轴分别交于点A,B.在y轴左侧有一点P(﹣1,a).
(1)如图1,以线段AB为直角边在第一象限内作等腰Rt△ABC,且∠BAC=90°,求点C的坐标;
(2)当a=![]() 时,求△ABP的面积;
时,求△ABP的面积;
(3)当a=﹣2时,点Q是直线y=﹣2x+2上一点,且△POQ的面积为5,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛” ![]() 为此,他对两位同学进行了辅导,并在辅导期间测验了10次,测验成绩如下表:
为此,他对两位同学进行了辅导,并在辅导期间测验了10次,测验成绩如下表:
第1次 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
甲 | 68 | 80 | 78 | 79 | 78 | 84 | 81 | 83 | 77 | 92 |
乙 | 86 | 80 | 75 | 83 | 79 | 80 | 85 | 80 | 77 | 75 |
利用表中数据,解答下列问题:
![]() 填空完成下表:
填空完成下表:
平均成绩 | 中位数 | 众数 | |
甲 | 80 |
| |
乙 | 80 | 80 |
![]() 张老师从测验成绩表中,求得甲的方差
张老师从测验成绩表中,求得甲的方差![]() ,请你计算乙10次测验成绩的方差.
,请你计算乙10次测验成绩的方差.
![]() 请你根据上面的信息,运用所学统计知识,帮张老师选拔出参加“全国数学联赛”的人选,并简要说明理由.
请你根据上面的信息,运用所学统计知识,帮张老师选拔出参加“全国数学联赛”的人选,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.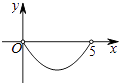
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年11月13日巴基斯坦瓜达尔港正式开港,此港成为我国“一带一路”必展战略上的一颗璀璨的明星,某大型远洋运输集团有三种型号的远洋货轮,每种型号的货轮载重量和盈利情况如下表所示:
甲 | 乙 | 丙 | |
平均货轮载重的吨数(万吨) | 10 | 5 | 7.5 |
平均每吨货物可获例如(百元) | 5 | 3.6 | 4 |
(1)若用乙、丙两种型号的货轮共8艘,将55万吨的货物运送到瓜达尔港,问乙、丙两种型号的货轮各多少艘?
(2)集团计划未来用三种型号的货轮共20艘装运180万吨的货物到国内,并且乙、丙两种型号的货轮数量之和不超过甲型货轮的数量,如果设丙型货轮有m艘,则甲型货轮有艘,乙型货轮有艘(用含有m的式子表示),那么如何安排装运,可使集团获得最大利润?最大利润的多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市同价销售同一款可拆分式驱蚊器,1套驱蚊器由1个加热器和1瓶电热蚊香液组成.电热蚊香液作为易耗品可单独购买,1瓶电热蚊香液的售价是1套驱蚊器的![]() .已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
.已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
(1)求1套驱蚊器和1瓶电热蚊香液的售价;
(2)为了促进该款驱蚊器的销售,甲超市打8.5折销售,而乙超市采用的销售方法是顾客每买1套驱蚊器送1瓶电热蚊香液.在这段促销期间,甲超市销售2000套驱蚊器,而乙超市在驱蚊器销售上获得的利润不低于甲超市的1.2倍.问乙超市至少销售多少套驱蚊器?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com