
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.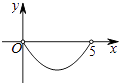
D.
【答案】D
【解析】解:如图,连接DE,∵△PC′D是△PCD沿PD折叠得到,
∴∠CPD=∠C′PD,
∵PE平分∠BPC′,
∴∠BPE=∠C′PE,
∴∠EPC′+∠DPC′= ![]() ×180°=90°,
×180°=90°,
∴△DPE是直角三角形,
∵BP=x,BE=y,AB=3,BC=5,
∴AE=AB﹣BE=3﹣y,CP=BC﹣BP=5﹣x,
在Rt△BEP中,PE2=BP2+BE2=x2+y2 ,
在Rt△ADE中,DE2=AE2+AD2=(3﹣y)2+52 ,
在Rt△PCD中,PD2=PC2+CD2=(5﹣x)2+32 ,
在Rt△PDE中,DE2=PE2+PD2 ,
则(3﹣y)2+52=x2+y2+(5﹣x)2+32 ,
整理得,﹣6y=2x2﹣10x,
所以y=﹣ ![]() x2+
x2+ ![]() x(0<x<5),
x(0<x<5),
纵观各选项,只有D选项符合.
故选:D.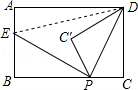
连接DE,根据折叠的性质可得∠CPD=∠C′PD,再根据角平分线的定义可得∠BPE=∠C′PE,然后证明∠DPE=90°,从而得到△DPE是直角三角形,再分别表示出AE、CP的长度,然后利用勾股定理进行列式整理即可得到y与x的函数关系式,根据函数所对应的图象即可得解.


科目:初中数学 来源: 题型:
【题目】某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
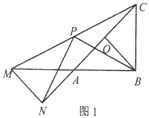
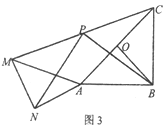
【题目】已知,△AOB中,AB=BC=2,∠ABC=90°,点O是线段AC的中点,连接OB,将△AOB绕点A逆时针旋转α度得到△ANM,连接CM,点P是线段CM的中点,连接PN、PB.
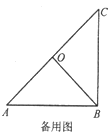
(1)如图1,当α=180°时,直接写出线段PN和PB之间的位置关系和数量关系;
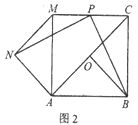
(2)如图2,当α=90°时,探究线段PN和PB之间的位置关系和数量关系,并给出完整的证明过程;
(3)如图3,直接写出当△AOB在绕点A逆时针旋转的过程中,线段PN的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.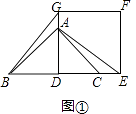
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)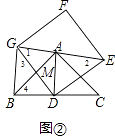
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:
①四边形AEGF是菱形 ②△AED≌△GED
③∠DFG=112.5° ④BC+FG=1.5
其中正确的结论是( )
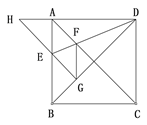
A. ①②③④ B. ①②③ C. ①② D. ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com