
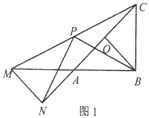
����Ŀ����֪����AOB�У�AB=BC=2,��ABC=90�㣬��O���߶�AC���е㣬����OB������AOB�Ƶ�A��ʱ����ת���ȵõ���ANM������CM����P���߶�CM���е㣬����PN��PB.
��1����ͼ1������=180��ʱ��ֱ��д���߶�PN��PB֮���λ�ù�ϵ��������ϵ��
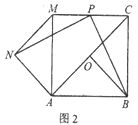
��2����ͼ2������=90��ʱ��̽���߶�PN��PB֮���λ�ù�ϵ��������ϵ��������������֤�����̣�
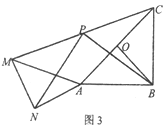
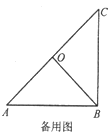
��3����ͼ3��ֱ��д������AOB���Ƶ�A��ʱ����ת�Ĺ����У��߶�PN�����ֵ����Сֵ��
���𰸡�(1)PN=PB��PN��PB��(2)�ԣ�(3) ![]()
����������1������ת�����ʿɵ���ABC�ա�ANM,����ֱ��������б�ߵ����ߵ���б�ߵ�һ�룬�õ�PN��![]() ֮���λ�ù�ϵ��������ϵ����2������һ����֤���ķ����루1��һ������3������OP�����ù��ɶ����ɵó��߶�PN�����ֵ����Сֵ.
֮���λ�ù�ϵ��������ϵ����2������һ����֤���ķ����루1��һ������3������OP�����ù��ɶ����ɵó��߶�PN�����ֵ����Сֵ.
�⣺��![]() ��
��![]() ��
�� ![]() ��
��
��![]() ������
������![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
�� ![]() ,
,
�֡�![]() ,
,
���ı���![]() Ϊ�����Σ�
������
��![]() Ϊ
Ϊ![]() �е㣬
�е㣬 ![]() Ϊ
Ϊ![]() �е㣬
�е㣬
��![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ������
������![]() ��
��
��![]() ��
�� ![]() Ϊ
Ϊ![]() ��
�� ![]() �е㣬
�е㣬
��![]() ��
��
��![]() ����
����
��![]() ��
�� ![]() ��
��
��![]() ��
��
![]() ��
��
��![]() ��
��
��![]() ��
��
![]() ���ֵΪ
���ֵΪ![]() ����СֵΪ
����СֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ![]() ��ƽ��ֱ������ϵ
��ƽ��ֱ������ϵ![]() �е�λ����ͼ��ʾ.
�е�λ����ͼ��ʾ.
(1)��![]() ���ڵ�
���ڵ�![]() �����ĶԳƵ�
�����ĶԳƵ�![]() .
.
(2)��![]() ����ƽ��4����λ������ƽ�ƺ��
����ƽ��4����λ������ƽ�ƺ��![]() .
.
(3)��![]() ��������һ��
��������һ��![]() ��ʹ
��ʹ![]() ��ֵ��С
��ֵ��С

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ҫ���������֤����
��֪����ͼ��AB��CD��ֱ��AE��CD�ڵ�C����BAC+��CDF=180��.

��֤��AE��DF.
֤���� ��AB��CD��____________________________�� ��
���BAC=��DCE��__________________________________________________________________________��.
����BAC+��CDF=180��(��֪)��
��____________ +��CDF=180����____________________________________��.
��AE��DF��______________________________________________________________________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�����ؼƻ�װ�˼ס��ҡ�������ˮ����������ۣ�ÿ�������涨���أ�����ֻװһ��ˮ���������Ϊװ�˼ס��ҡ�������ˮ��������������
�� | �� | �� | |
ÿ��������װ���������֣� | 4 | 2 | 3 |
ÿ��ˮ���ɻ�����ǧԪ�� | 5 | 7 | 4 |
��1����8������װ���ҡ�������ˮ����22�ֵ�A�����ۣ���װ���ҡ�������ˮ������������������
��2��ˮ�����ؼƻ���20������װ�˼ס��ҡ�������ˮ����72�ֵ�B�����ۣ�ÿ��ˮ��������һ����������װ�˼�ˮ��������Ϊm������װ���ҡ�������ˮ�������������������������m��ʾ��
��3���ڣ�2���ʵĻ����ϣ���ΰ���װ�˿�ʹˮ�����ػ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�������϶�Ӧ����Ϊ2������BҲ�������������߶�AB�ij�Ϊ4��CΪAB���е������C�������϶�Ӧ����Ϊ________��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�����1����ABC�Ķ��㶼������������ĸ�㣨�����ߵĽ��㣩�ϣ�
��1��������ͼ��ʾ������ƽ��������ƽ��ֱ������ϵ��ʹ��A����Ϊ��1��3����B����Ϊ��2��1����
��2����������ABC����y��ԳƵġ�A'B'C'����д����C'�����ꣻ
��3���жϡ�ABC����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=��2x+2��ͼ����x�ᡢy��ֱ��ڵ�A��B����y�������һ��P����1��a����
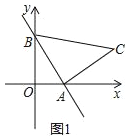
��1����ͼ1�����߶�ABΪֱ�DZ��ڵ�һ������������Rt��ABC���ҡ�BAC=90�������C�����ꣻ
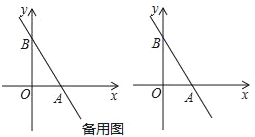
��2����a=![]() ʱ�����ABP�������
ʱ�����ABP�������
��3����a=��2ʱ����Q��ֱ��y=��2x+2��һ�㣬�ҡ�POQ�����Ϊ5�����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=3��BC=5����P��BC���ϵ�һ�����㣨��P�����B��C�غϣ����ֽ���PCD��ֱ��PD�۵���ʹ��C�䵽��C�䴦������BPC��Ľ�ƽ���߽�AB�ڵ�E����BP=x��BE=y��������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ� ��
A.
B.
C.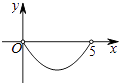
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABC�У�ADƽ�֡�BAC��AD��BC������ΪD��AN����ABC��ǡ�CAM��ƽ���ߣ�CE��AN������ΪE.
��1����֤���ı���ADCE�Ǿ��Σ�
��2������ABC����ʲô����ʱ���ı���ADCE�������Σ�����֤��.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com