
【题目】按要求完成下列证明:
已知:如图,AB∥CD,直线AE交CD于点C,∠BAC+∠CDF=180°.

求证:AE∥DF.
证明: ∵AB∥CD(____________________________) ,
∴∠BAC=∠DCE(__________________________________________________________________________).
∵∠BAC+∠CDF=180°(已知),
∴____________ +∠CDF=180°(____________________________________).
∴AE∥DF(______________________________________________________________________).
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在 △ABC 中,∠C=90°,DB⊥BC 于点 ,分别以点 D 和点 为圆心,以大于![]() 的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
因为 DB⊥BC(已知),
所以 ∠DBC=90°( ) .
因为 ∠C=90°(已知),
所以 ∠DBC=∠C(等量代换),
所以 DB∥AC ( ) ,
所以 (两直线平行,同位角相等);
由作图法可知:直线 EF 是线段 DB 的 ( ) ,
所以 GD=GB,线段 (上的点到线段两端点的距离相等),
所以 ( ) ,因为 ∠A=∠1(已知),
所以 ∠A=∠D(等量代换).

查看答案和解析>>
科目:初中数学 来源: 题型:
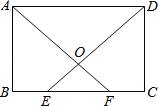
【题目】(10分)如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.
求证:(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论: ①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )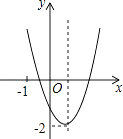
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点A,给出如下定义:若存在点B(不与点A重合,且直线AB不与坐标轴平行或重合),过点A作直线m∥x轴,过点B作直线n∥y轴,直线m,n相交于点C.当线段AC,BC的长度相等时,称点B为点A 的等距点,称三角形ABC的面积为点A的等距面积. 例如:如图,点A(2,1),点B(5,4),因为AC= BC=3,所以B为点A 的等距点,此时点A的等距面积为![]() .
.
(1)点A的坐标是(0,1),在点B1(-1,0),B2(2,3),B3(-1,-1)中,点A 的等距点为________________.
(2)点A的坐标是(-3,1),点A的等距点B在第三象限,
①若点B的坐标是![]() ,求此时点A的等距面积;
,求此时点A的等距面积;
②若点A的等距面积不小于![]() ,求此时点B的横坐标t的取值范围.
,求此时点B的横坐标t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
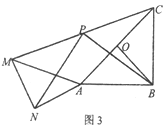
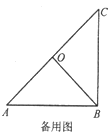
【题目】已知,△AOB中,AB=BC=2,∠ABC=90°,点O是线段AC的中点,连接OB,将△AOB绕点A逆时针旋转α度得到△ANM,连接CM,点P是线段CM的中点,连接PN、PB.
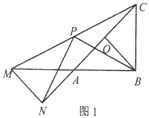
(1)如图1,当α=180°时,直接写出线段PN和PB之间的位置关系和数量关系;
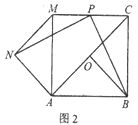
(2)如图2,当α=90°时,探究线段PN和PB之间的位置关系和数量关系,并给出完整的证明过程;
(3)如图3,直接写出当△AOB在绕点A逆时针旋转的过程中,线段PN的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com