
【题目】对于平面直角坐标系xOy中的点A,给出如下定义:若存在点B(不与点A重合,且直线AB不与坐标轴平行或重合),过点A作直线m∥x轴,过点B作直线n∥y轴,直线m,n相交于点C.当线段AC,BC的长度相等时,称点B为点A 的等距点,称三角形ABC的面积为点A的等距面积. 例如:如图,点A(2,1),点B(5,4),因为AC= BC=3,所以B为点A 的等距点,此时点A的等距面积为![]() .
.
(1)点A的坐标是(0,1),在点B1(-1,0),B2(2,3),B3(-1,-1)中,点A 的等距点为________________.
(2)点A的坐标是(-3,1),点A的等距点B在第三象限,
①若点B的坐标是![]() ,求此时点A的等距面积;
,求此时点A的等距面积;
②若点A的等距面积不小于![]() ,求此时点B的横坐标t的取值范围.
,求此时点B的横坐标t的取值范围.

科目:初中数学 来源: 题型:
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中![]() 的变化情况,解答下列问题.
的变化情况,解答下列问题.
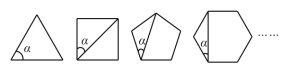
(1)将下面的表格补充完整:

(2)根据规律,是否存在一个正n边形,使其中的![]() ?若存在,直接写出
?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的![]() ?若存在,直接写出
?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列证明:
已知:如图,AB∥CD,直线AE交CD于点C,∠BAC+∠CDF=180°.

求证:AE∥DF.
证明: ∵AB∥CD(____________________________) ,
∴∠BAC=∠DCE(__________________________________________________________________________).
∵∠BAC+∠CDF=180°(已知),
∴____________ +∠CDF=180°(____________________________________).
∴AE∥DF(______________________________________________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,E为AB边上一点, ∠BCE=15°,EF∥AD交DC于点F.
(1)依题意补全图形,求∠FEC的度数;
(2)若∠A=140°,求∠AEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
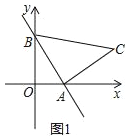
【题目】一次函数y=﹣2x+2的图象与x轴、y轴分别交于点A,B.在y轴左侧有一点P(﹣1,a).
(1)如图1,以线段AB为直角边在第一象限内作等腰Rt△ABC,且∠BAC=90°,求点C的坐标;
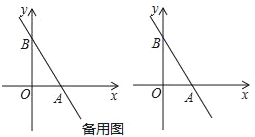
(2)当a=![]() 时,求△ABP的面积;
时,求△ABP的面积;
(3)当a=﹣2时,点Q是直线y=﹣2x+2上一点,且△POQ的面积为5,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com