
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中![]() 的变化情况,解答下列问题.
的变化情况,解答下列问题.
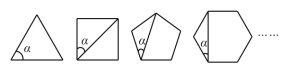
(1)将下面的表格补充完整:

(2)根据规律,是否存在一个正n边形,使其中的![]() ?若存在,直接写出
?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的![]() ?若存在,直接写出
?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:初中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
【答案】B
【解析】解析:∵2a4+2b4+c4=2a2c2+2b2c2,∴4a4-4a2c2+c4+4b4-4b2c2+c4=0,
∴(2a2-c2)2+(2b2-c2)2=0,∴2a2-c2=0,2b2-c2=0,
∴c=2a,c=2b,
∴a=b,且a2+b2=c2,
∴△ABC为等腰直角三角形.
故选B.
【题型】单选题
【结束】
11
【题目】将图1中阴影部分的小长方形变换到图2的位置,你能根据两个图形的面积关系得到的数学公式是_____.
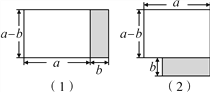
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以菱形ABCD对角线交点为坐标原点,建立平面直角坐标系,A、B两点的坐标分别为(﹣2 ![]() ,0)、(0,﹣
,0)、(0,﹣ ![]() ),直线DE⊥DC交AC于E,动点P从点A出发,以每秒2个单位的速度沿着A→D→C的路线向终点C匀速运动,设△PDE的面积为S(S≠0),点P的运动时间为t秒.
),直线DE⊥DC交AC于E,动点P从点A出发,以每秒2个单位的速度沿着A→D→C的路线向终点C匀速运动,设△PDE的面积为S(S≠0),点P的运动时间为t秒.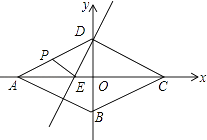
(1)求直线DE的解析式;
(2)求S与t之间的函数关系式,并写出自变量t的取值范围;
(3)当t为何值时,∠EPD+∠DCB=90°?并求出此时直线BP与直线AC所夹锐角的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 △ABC 中,∠C=90°,DB⊥BC 于点 ,分别以点 D 和点 为圆心,以大于![]() 的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
因为 DB⊥BC(已知),
所以 ∠DBC=90°( ) .
因为 ∠C=90°(已知),
所以 ∠DBC=∠C(等量代换),
所以 DB∥AC ( ) ,
所以 (两直线平行,同位角相等);
由作图法可知:直线 EF 是线段 DB 的 ( ) ,
所以 GD=GB,线段 (上的点到线段两端点的距离相等),
所以 ( ) ,因为 ∠A=∠1(已知),
所以 ∠A=∠D(等量代换).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】云南地区地震发生后,市政府筹集了必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能求出这三种车型分别有多少辆吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 与一次函数y=ax+b的图象交于点A(2,2)、B(
与一次函数y=ax+b的图象交于点A(2,2)、B( ![]() ,n).
,n). 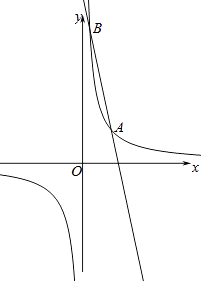
(1)求这两个函数解析式;
(2)将一次函数y=ax+b的图象沿y轴向下平移m个单位,使平移后的图象与反比例函数y= ![]() 的图象有且只有一个交点,求m的值.
的图象有且只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.
求证:(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
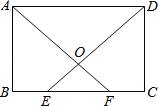
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点A,给出如下定义:若存在点B(不与点A重合,且直线AB不与坐标轴平行或重合),过点A作直线m∥x轴,过点B作直线n∥y轴,直线m,n相交于点C.当线段AC,BC的长度相等时,称点B为点A 的等距点,称三角形ABC的面积为点A的等距面积. 例如:如图,点A(2,1),点B(5,4),因为AC= BC=3,所以B为点A 的等距点,此时点A的等距面积为![]() .
.
(1)点A的坐标是(0,1),在点B1(-1,0),B2(2,3),B3(-1,-1)中,点A 的等距点为________________.
(2)点A的坐标是(-3,1),点A的等距点B在第三象限,
①若点B的坐标是![]() ,求此时点A的等距面积;
,求此时点A的等距面积;
②若点A的等距面积不小于![]() ,求此时点B的横坐标t的取值范围.
,求此时点B的横坐标t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com