
����Ŀ����ͼ��������ABCD�Խ��߽���Ϊ����ԭ�㣬����ƽ��ֱ������ϵ��A��B���������ֱ�Ϊ����2 ![]() ��0������0����
��0������0���� ![]() ����ֱ��DE��DC��AC��E������P�ӵ�A��������ÿ��2����λ���ٶ�����A��D��C��·�����յ�C�����˶������PDE�����ΪS��S��0������P���˶�ʱ��Ϊt�룮
����ֱ��DE��DC��AC��E������P�ӵ�A��������ÿ��2����λ���ٶ�����A��D��C��·�����յ�C�����˶������PDE�����ΪS��S��0������P���˶�ʱ��Ϊt�룮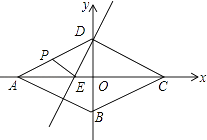
��1����ֱ��DE�Ľ���ʽ��
��2����S��t֮��ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3����tΪ��ֵʱ����EPD+��DCB=90�㣿�������ʱֱ��BP��ֱ��AC������ǵ�����ֵ��
���𰸡�
��1��
�⣺�����εĶԳ��Կɵã�C��2 ![]() ��0����D��0��
��0����D��0�� ![]() ����
����
��OD= ![]() ��OC=2
��OC=2 ![]() ��tan��DCO=
��tan��DCO= ![]() =
= ![]() ��
��
��DE��DC��
���EDO+��CDO=90�㣬
�ߡ�DCO+��CD��=90�㣬
���EDO=��DCO��
��tan��EDO=tan��DCO= ![]() ��
��
�� ![]() ��
��
��OE= ![]() ��
��
��E���� ![]() ��0����
��0����
��D��0�� ![]() ����
����
��ֱ��DE����ʽΪy=2x+ ![]()
��2��
�⣺�ɣ�1����E���� ![]() ��0����
��0����
��AE=AO��OE=2 ![]() ��
�� ![]() =
= ![]() ��
��
���ݹ��ɶ����ã�DE= ![]() =
= ![]() ��
��
�����εı߳�Ϊ5��
��ͼ1��
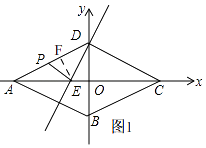
����E��EF��AD��
��sin��DAO= ![]() ��
��
��EF= ![]() =
= ![]() ��
��
����P��AD�����˶�����0��t�� ![]() ��
��
S= ![]() PD��EF=
PD��EF= ![]() ����5��2t����
����5��2t���� ![]() =��
=�� ![]() t+
t+ ![]() ��
��
��ͼ2��
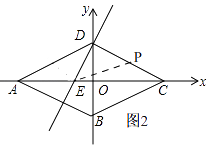
��P��DC�����˶�ʱ���� ![]() ��t��5ʱ��
��t��5ʱ��
S= ![]() PD��DE=
PD��DE= ![]() ����2t��5����
����2t��5���� ![]() =
= ![]() t��
t�� ![]() ��
��
��S= 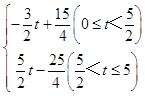
��3��
�⣺��BP��AC�ཻ�ڵ�Q��
������ABCD����DAB=��DCB��DE��DC��
��DE��AB��
���DAB+��ADE=90�㣬
���DCB+��ADE=90�㣬
��Ҫʹ��EPD+��DCB=90�㣬
���EPD=��ADE��
����P��AD���˶�ʱ����ͼ3��
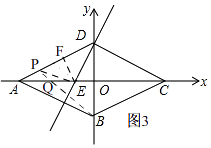
�ߡ�EPD=��ADE��
��EF��ֱƽ����PD��
��AP=AD��2DF=AD��2 ![]() ��
��
��2t=5�� ![]() ��
��
��t= ![]() ��
��
��ʱAP=1��
��AP��BC��
���APQ�ס�CBQ��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
��AQ= ![]() ��
��
��OQ=OA��AQ= ![]() ��
��
��Rt��OBQ��tan��OQB= ![]() =
= ![]() =
= ![]() ��
��
����P��DC���˶�ʱ����ͼ4��
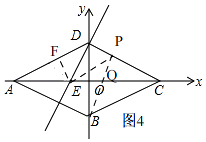
�ߡ�EPD=��ADE����EDP=��EFD=90��
���EDP�ס�EFD��
�� ![]() ��
��
��DP= ![]() =
= 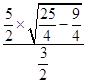 =
= ![]() ��
��
��2t=AD��DP=5+ ![]() ��
��
��t= ![]() ��
��
��ʱCP=DC��DP=5�� ![]() =
= ![]() ��
��
��PC��AB��
���CPQ�ס�ABQ��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
��CQ= ![]() ��
��
��OQ=OC��CQ=2 ![]() ��
�� ![]() =
= ![]() ��
��
��Rt��OBD��tan��OQB= ![]() =
= ![]() =1��
=1��
������t= ![]() ʱ����EPD+��DCB=90�㣮��ʱֱ��BP��ֱ��AC������ǵ�����ֵΪ
ʱ����EPD+��DCB=90�㣮��ʱֱ��BP��ֱ��AC������ǵ�����ֵΪ ![]() ��
��
��t= ![]() ʱ����EPD+��DCB=90�㣮��ʱֱ��BP��ֱ��AC������ǵ�����ֵΪ1
ʱ����EPD+��DCB=90�㣮��ʱֱ��BP��ֱ��AC������ǵ�����ֵΪ1
����������1���������εĶԳ��Եó���C��D���꣬Ȼ���á�DCO������ֵ���Լ��Ƚǵ����Ǻ���ֵ����г����̣�����ô���ϵ�������ֱ��DE����ʽ����2����������εı߳��������EF���ֵ�P��AD��DC���ϣ��������ʽ��⣻��3���������EPD=��ADE������������������εı߳������������ʱ��t�������������εı���ʽ�����������OQ����ֱ�������μ��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ʒ�ı��۸���200Ԫ�������ż��ڵı仯����Ʒ�ļ۸�ɸ���![]() ����һ�룮
����һ�룮
![]() �ĺ�����ʲô��
�ĺ�����ʲô��
![]() ������������Ʒ����۸����ͼ۸�
������������Ʒ����۸����ͼ۸�
![]() ����Ա���Ϊ�����������ۼǡ�
����Ա���Ϊ�����������ۼǡ�![]() �������ڱ��ۼǡ�
�������ڱ��ۼǡ�![]() ��������Ʒ�۸�ĸ�����Χ�ֿ���������ʾ��
��������Ʒ�۸�ĸ�����Χ�ֿ���������ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��AB=AC=4����C=72�㣬D��AB�е㣬��E��AC�ϣ�DE��AB����cosA��ֵΪ�� �� 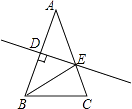
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�DZ߳�Ϊ4 ![]() �ĵȱߡ�ABC�����ģ�����OBC�Ƶ�O��ʱ����ת30��õ���OB1C1 �� B1C1��BC�ڵ�D��B1C1��AC�ڵ�E����DE= ��
�ĵȱߡ�ABC�����ģ�����OBC�Ƶ�O��ʱ����ת30��õ���OB1C1 �� B1C1��BC�ڵ�D��B1C1��AC�ڵ�E����DE= �� 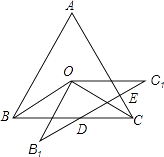
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��Oֱ����CΪ��O��һ�㣬��D�� ![]() ���е㣬DE��AC��E��DF��AB��F��
���е㣬DE��AC��E��DF��AB��F�� 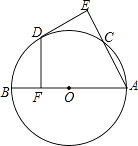
��1���ж�DE���O��λ�ù�ϵ����֤����Ľ��ۣ�
��2����OF=4����AC�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ʵ��ע���ذ�ƶ����ͥѧ����ijУ��ȫУ����ƶ����ͥѧ�����������������ͳ�ƣ��Ա���Ҿ���ƶ������Ч��ʵ��ͳ�Ʒ��ְ���ƶ����ͥѧ�������ֱ���2����3����4����5����6����������������������Ƴ�������������������ͳ��ͼ�� 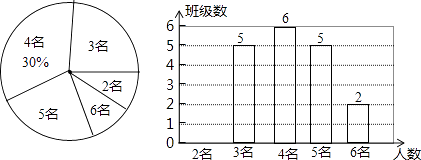
��1�����Уһ���ж��ٸ��ࣿ��������ͼ����������
��2��ij������ʿ������2��ƶ����ͥѧ������Щ�༶�У���ѡ�������а���������б�������״ͼ�ķ����������ѡ�е�����ѧ������ͬһ�༶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������n��nΪ��������������x��һԪ���η��̣� ��x2��1=0����x2+x��2=0����x2+2x��3=0����x2+3x��4=0����������
��1������һԪ���η��̵Ľ�Ϊ��________����________����________����________��
��2�����룺��n������Ϊ________�����Ϊ________��
��3������ָ����n�����̵ĸ���ʲô��ͬ���ص㣨д��һ�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ������εĸ��߶���ȣ��Ҹ��ڽ�Ҳ����ȣ���ô�������ξͽ���������Σ���ͼ������һ��������Σ��۲�ÿ�����������![]() �ı仯���������������⣮
�ı仯���������������⣮
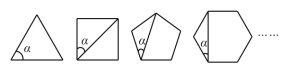
��1��������ı���������

��2�����ݹ��ɣ��Ƿ����һ����n���Σ�ʹ���е�![]() �������ڣ�ֱ��д��
�������ڣ�ֱ��д��![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��3�����ݹ��ɣ��Ƿ����һ����n���Σ�ʹ���е�![]() �������ڣ�ֱ��д��
�������ڣ�ֱ��д��![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������ABCO�Ƶ�C��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������CDEF��ED���߶�AB�ڵ�G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��

��1����֤����CBG�ա�CDG��
��2������HCG�Ķ��������ж��߶�HG��OH��BG֮���������ϵ��˵�����ɣ�
��3������BD��DA��AE��EB�õ��ı���AEBD������ת�����У��ı���AEBD�ܷ�Ϊ���Σ�����ܣ��������H�����ꣻ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com