
【题目】如图,在 △ABC 中,∠C=90°,DB⊥BC 于点 ,分别以点 D 和点 为圆心,以大于![]() 的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
因为 DB⊥BC(已知),
所以 ∠DBC=90°( ) .
因为 ∠C=90°(已知),
所以 ∠DBC=∠C(等量代换),
所以 DB∥AC ( ) ,
所以 (两直线平行,同位角相等);
由作图法可知:直线 EF 是线段 DB 的 ( ) ,
所以 GD=GB,线段 (上的点到线段两端点的距离相等),
所以 ( ) ,因为 ∠A=∠1(已知),
所以 ∠A=∠D(等量代换).

【答案】垂直的定义;内错角相等,两直线平行;∠A;∠1;垂直平分线;垂直平分线;∠1;∠D;等边对等角
【解析】先利用平行线的判定方法证明DB∥AC,则根据平行线的性质得到∠A=∠1;由作图法可知直线EF是线段DB的垂直平分线,则GD=GB,所以∠1=∠D,然后利用等两代换得到∠A=∠D.
因为DB⊥BC(已知)
所以∠DBC=90°(垂直的定义)①
因为∠C=90°(已知)
所以∠DBC=∠C(等量代换)
所以DB∥AC(内错角相等,两直线平行)②
所以∠A=∠1③(两直线平行,同位角相等);
由作图法可知:直线EF是线段DB的(垂直平分线)④
所以GD=GB(线段垂直平分线上的点到线段两端点的距离相等)⑤
所以∠1=∠D(等边对等角)⑥,
因为∠A=∠1(已知)
所以∠A=∠D(等量代换).
故答案为垂直的定义;内错角相等,两直线平行;∠A,∠1;垂直平分线;垂直平分线;∠1,∠D;等边对等角.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y= ![]() 过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
(1)根据现有的信息,请求出题中的一次函数的解析式.
(2)根据关系式画出这个函数图象.
(3)过点B能不能画出一直线BC将△ABO(O为坐标原点)分成面积比为1:2的两部分?如能,可以画出几条,并求出其中一条直线所对应的函数关系式,其它的直接写出函数关系式;若不能,说明理由.
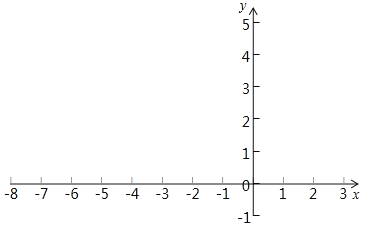
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是边长为4 ![]() 的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1 , B1C1交BC于点D,B1C1交AC于点E,则DE= .
的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1 , B1C1交BC于点D,B1C1交AC于点E,则DE= . 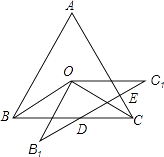
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,以便国家精准扶贫政策有效落实.统计发现班上贫困家庭学生人数分别有2名、3名、4名、5名、6名,共五种情况.并将其制成了如下两幅不完整的统计图: 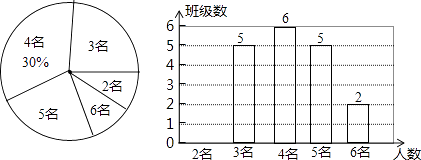
(1)求该校一共有多少个班?并将条形图补充完整;
(2)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表法或树状图的方法,求出被选中的两名学生来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,下列n(n为正整数)个关于x的一元二次方程: ①x2﹣1=0,②x2+x﹣2=0,③x2+2x﹣3=0,④x2+3x﹣4=0,…,,…
(1)上述一元二次方程的解为①________,②________,③________,④________.
(2)猜想:第n个方程为________,其解为________.
(3)请你指出这n个方程的根有什么共同的特点(写出一条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中![]() 的变化情况,解答下列问题.
的变化情况,解答下列问题.
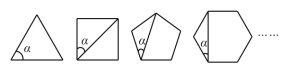
(1)将下面的表格补充完整:

(2)根据规律,是否存在一个正n边形,使其中的![]() ?若存在,直接写出
?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的![]() ?若存在,直接写出
?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 ![]() 在平面直角坐标系
在平面直角坐标系![]() 中的位置如图所示.
中的位置如图所示.
(1)作![]() 关于点
关于点![]() 成中心对称的
成中心对称的![]() .
.
(2)将![]() 向右平移4个单位,作出平移后的
向右平移4个单位,作出平移后的![]() .
.
(3)在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的值最小
的值最小

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列证明:
已知:如图,AB∥CD,直线AE交CD于点C,∠BAC+∠CDF=180°.

求证:AE∥DF.
证明: ∵AB∥CD(____________________________) ,
∴∠BAC=∠DCE(__________________________________________________________________________).
∵∠BAC+∠CDF=180°(已知),
∴____________ +∠CDF=180°(____________________________________).
∴AE∥DF(______________________________________________________________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com