
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( ) 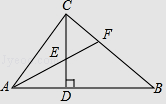
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:过点F作FG⊥AB于点G, 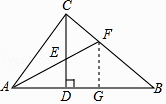
∵∠ACB=90°,CD⊥AB,
∴∠CDA=90°,
∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,
∵AF平分∠CAB,
∴∠CAF=∠FAD,
∴∠CFA=∠AED=∠CEF,
∴CE=CF,
∵AF平分∠CAB,∠ACF=∠AGF=90°,
∴FC=FG,
∵∠B=∠B,∠FGB=∠ACB=90°,
∴△BFG∽△BAC,
∴ ![]() =
= ![]() ,
,
∵AC=3,AB=5,∠ACB=90°,
∴BC=4,
∴ ![]() =
= ![]() ,
,
∵FC=FG,
∴ ![]() =
= ![]() ,
,
解得:FC= ![]() ,
,
即CE的长为 ![]() .
.
故选:A.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品每天的利润为y元。
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天的销售利润不低于4800元?请直接写出结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=10,∠B=60°,∠C=45°,则点A到BC的距离是( )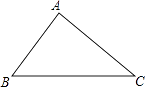
A.10﹣5 ![]()
B.5+5 ![]()
C.15﹣5 ![]()
D.15﹣10 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值 ![]() ﹣1.其中正确的说法有( )个.
﹣1.其中正确的说法有( )个.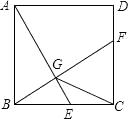
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).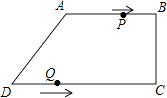
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com