
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值 ![]() ﹣1.其中正确的说法有( )个.
﹣1.其中正确的说法有( )个.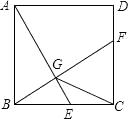
A.4
B.3
C.2
D.1
【答案】C
【解析】解答】∵四边形ABCD为正方形,BF⊥AE,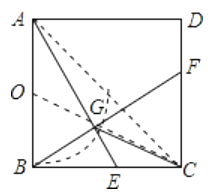
∴∠AGB=90°,
∴G点在以AB为直径,AB中点O为圆心的圆弧上,
∴当点E移动到与C重合时,F点与D点重合,此时G为AC中点,
∴AG=GE,
故①错误.
∵当点E运动到C点时停止,
∴点G运动的轨迹为![]() 圆,
圆,
又∵正方形ABCD的边长为2,
∴圆弧的长为:![]() ×2×
×2×![]() ×1=
×1=![]()
![]() .
.
故③错误.
∵四边形ABCD为正方形,
∴AB=BC,∠ABC=∠BCF=90°,
又∵BF⊥AE,
∴∠AGB=90°,
即∠ABG+∠GBE=90°,
∴∠BAG+∠ABG=90°,
∴∠GBE=∠BAG,
在△ABE和△BCF中,
∵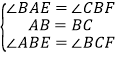 ,
,
∴△ABE≌△BCF,
∴AE=BF,
故②正确.
当O、G、C三点共线时,CG取得最小,
∵OB=1,BC=2,
∴OC=![]() =
=![]() ,
,
∴CG=OC-OG=![]() -1,
-1,
故④正确.
所以答案是:C.
①由题意得∠AGB=90°,G点在以AB为直径,AB中点O为圆心的圆弧上;故当E移动到与C重合时,F点与D点重合,此时G为AC中点,故①错误.
②由正方形的性质得出,AB=BC,∠ABC=∠BCF=90°,再由同角的余角相等得出∠GBE=∠BAG,再利用ASA得出△ABE≌△BCF,根据全等三角形性质得出AE=BF,故②正确.
②当点E运动到C点时停止,此时点G运动的轨迹为![]() 圆,从而得出②错误.
圆,从而得出②错误.
④当O、G、C三点共线时,CG取得最小,根据勾股定理得出OC的长度,再由CG=OC-OG得出④正确.
【考点精析】通过灵活运用勾股定理的概念和正方形的性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】下列函数关系中,属于正比例函数关系的是( )
A.圆的面积与它的半径
B.面积为常数S时矩形的长y与宽x
C.路程是常数时,行驶的速度v与时间t
D.三角形的底边是常数a时它的面积S与这条边上的高h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组数:1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,…其中每个数n都连续出现n次,那么这一组数的第119个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知∠APB=300,圆心O在边PB上, ⊙O 的半径为1cm,OP=3cm. 若⊙O 沿射线BP方向平移,当 ⊙O 与直线PA相切时,圆心O平移的距离为_________cm.
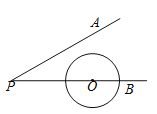
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( ) 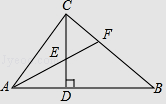
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com