
如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,
∠BAM=30°,AB=6m.
(1)求FM的长;
(2)连接AF,若sin∠FAM= ,求AM的长.
,求AM的长.

(1)9m;(2)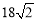 m.
m.
【解析】
试题分析:(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,根据AB∥CD∥EF,AM∥BC∥DE,构造并解Rt△ABN、Rt△DCG、Rt△FEH,求出BN、DG、FH的长度,继而可求出FM的长度.
(2)在Rt△FAM中,根据sin∠FAM=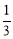 ,求出AF的长度,然后利用勾股定理求出AM的长度.
,求出AF的长度,然后利用勾股定理求出AM的长度.
试题解析:【解析】
(1)如答图,分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,
在Rt△ABN中,∵AB=6m,∠BAM=30°,
∴BN=ABsin∠BAN=6× =3m.
=3m.
∵AB∥CD∥EF,AM∥BC∥DE,同理可得:DG=FH=3m,∴FM=FH+DG+BN=9m.
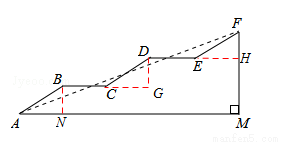
(2)在Rt△FAM中,∵FM=9m,sin∠FAM=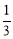 ,∴AF=27m.∴AM=
,∴AF=27m.∴AM=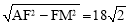 (m).
(m).
∴AM的长为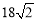 m.
m.
考点:1.解直角三角形的应用(坡度坡角问题);2.锐角三角函数定义;3.特殊角的三角函数值;4.勾股定理.


科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:解答题
我们用 表示不大于
表示不大于 的最大整数,例如:
的最大整数,例如: ,
, ,
, ;用
;用 表示大于
表示大于 的最小整数,例如:
的最小整数,例如: ,
, ,
,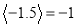 .解决下列问题:
.解决下列问题:
(1) = ,,
= ,, = ;
= ;
(2)若 =2,则
=2,则 的取值范围是 ;若
的取值范围是 ;若 =-1,则
=-1,则 的取值范围是 ;
的取值范围是 ;
(3)已知 ,
, 满足方程组
满足方程组 ,求
,求 ,
, 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:填空题
某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按3:3:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分,90分和85分,则他本学期数学学期综合成绩是 分.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
为了了解某市120000名初中学生的视力情况,某校数学兴趣小组,并进行整理分析.
(1)小明在眼镜店调查了1000名初中学生的视力,小刚在邻居中调查了20名初中学生的视力,他们的抽样是否合理?并说明理由.
(2)该校数学兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.
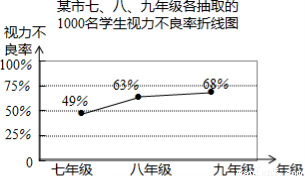
请你根据抽样调查的结果,估计该市120000名初中学生视力不良的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com