
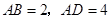 ,
,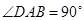 ,
,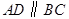 .
.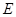 是射线
是射线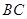 上的动点(点
上的动点(点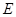 与点
与点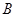 不重合),
不重合),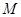 是线段
是线段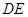 的中点.
的中点.
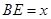 ,
,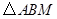 的面积为
的面积为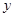 ,求
,求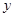 关于
关于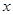 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;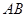 为直径的圆与以线段
为直径的圆与以线段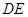 为直径的圆外切,求线段
为直径的圆外切,求线段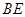 的长;
的长;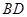 ,交线段
,交线段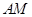 于点
于点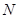 ,如果以
,如果以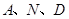 为顶点的三角形与
为顶点的三角形与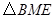 相似,求线段
相似,求线段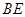 的长.
的长.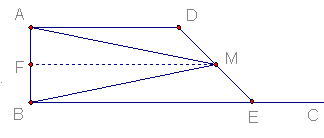
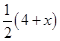 …………………………1分
…………………………1分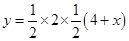
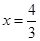
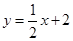 且
且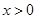 ………………3分
………………3分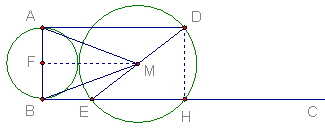
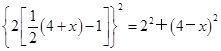 …………5分
…………5分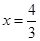 ……………………………………6分
……………………………………6分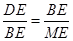
 ∴
∴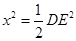
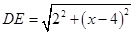
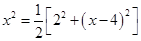
 ………………12分
………………12分

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:不详 题型:解答题
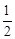 AC的长为半径在AC的两边作弧,交于点M、N;②连接MN,分别交AB、AC于点D、O;③过点C作CE∥AB交MN于点E,连接AE、CD.
AC的长为半径在AC的两边作弧,交于点M、N;②连接MN,分别交AB、AC于点D、O;③过点C作CE∥AB交MN于点E,连接AE、CD.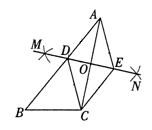
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.三角形的形状不变,三边的比变大 | B.三角形的形状变,三边的比变大 |
| C.三角形的形状变,三边的比不变 | D.三角形的形状不变,三边的比不变 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
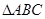 中,
中, ,
, ,
,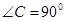 .
.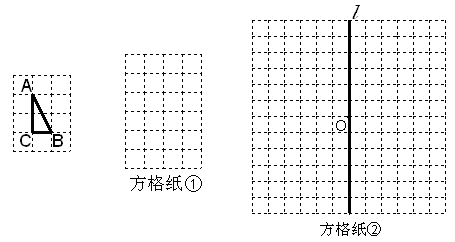
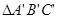 ,使
,使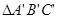 ∽
∽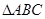 ,且相似比为2︰1;
,且相似比为2︰1;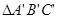 称为“基本图形”,请你利用“基本图形”,借助旋转、平移或轴对称变换,在方格纸②中设计一个以点
称为“基本图形”,请你利用“基本图形”,借助旋转、平移或轴对称变换,在方格纸②中设计一个以点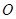 为对称中心,并且以直线
为对称中心,并且以直线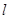 为对称轴的图案.
为对称轴的图案.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com