
【题目】小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小敏离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示.请根据图象回答下列问题:
(1)小敏去超市途中的速度是 ;在超市逗留了 ;
(2)小敏几点几分返回到家?
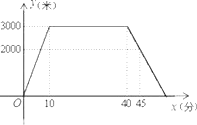
【答案】(1)速度为300米/分,逗留时间为30分钟.
(2)返回到家的时间为8:55.
【解析】试题分析:根据图形得出速度已经逗留的时间;首先设返回家时的函数解析式为y=kx+b,然后将(40,3000)和(45,2000)代入解析式求出函数解析式,然后求出y=0时x的值,从而得出返回家的时间.
试题解析:(1)速度为:3000÷10=300(米/分)
逗留的时间为:40-10=30(分钟)
(2)设返回家时,y与x的函数解析式为y=kx+b,把(40,3000),(45,2000)代入得:
![]() 解得:
解得: ![]() ∴函数解析式为:y=-200x+11000
∴函数解析式为:y=-200x+11000
当y=0时,x=55 ∴返回到家的时间为8:55.


科目:初中数学 来源: 题型:
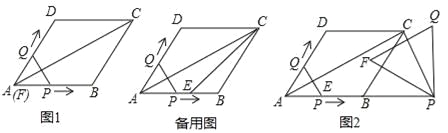
【题目】已知:如图1,菱形ABCD的边长为6,∠DAB=60°,点E是AB的中点,连接AC、EC.点Q从点A出发,沿折线A﹣D﹣C运动,同时点P从点A出发,沿射线AB运动,P、Q的速度均为每秒1个单位长度;以PQ为边在PQ的左侧作等边△PQF,△PQF与△AEC重叠部分的面积为S,当点Q运动到点C时P、Q同时停止运动,设运动的时间为t.
(1)当等边△PQF的边PQ恰好经过点D时,求运动时间t的值;当等边△PQF的边QF 恰好经过点E时,求运动时间t的值;
(2)在整个运动过程中,请求出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,当点Q到达C点时,将等边△PQF绕点P旋转α°(0<α<360),直线PF分别与直线AC、直线CD交于点M、N.是否存在这样的α,使△CMN为等腰三角形?若存在,请直接写出此时线段CM的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店将进货价为20元/盒的百合花,在市场参考价28~38元的范围内定价36元/盒销售,这样平均每天可售出40盒,经过市场调查发现,在进货价不变的情况下,若每盒下调1元,则平均每天可多销售10盒,要使每天的利润达到750元,应将每盒百合花在售价上下调多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=DC,AC=DB,AC与DB交于点M.过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N.
(1)求证:△ABC≌△DCB;
(2)求证:四边形BNCM是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,BC=6,AB=10.点Q与点B在AC的同侧,且AQ⊥AC.
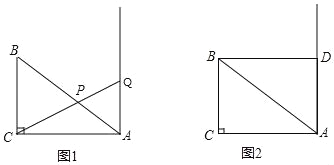
(1)如图1,点Q不与点A重合,连结CQ交AB于点P.设AQ=x,AP=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(2)是否存在点Q,使△PAQ与△ABC相似,若存在,求AQ的长;若不存在,请说明理由;
(3)如图2,过点B作BD⊥AQ,垂足为D.将以点Q为圆心,QD为半径的圆记为⊙Q.若点C到⊙Q上点的距离的最小值为8,求⊙Q的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.延长直线AB
B.在射线AM上顺次截取线段AC=CB=a
C.如果AC=BC,则点C为AB的中点
D.平角是一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球上的海洋面积约三亿六千一百万平方千米,用科学记数法表示为( )平方千米.
A. 361×106B. 36.1×107C. 3.61×108D. 0.361×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+![]() ,BC=2
,BC=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com