解:(1)∵关于x的方程(m
2-1)x
2-3(3m-1)x+18=0有两个正整数根(m是整数).
∵a=m
2-1,b=-9m+3,c=18,
∴b
2-4ac=(9m-3)
2-72(m
2-1)=9(m-3)
2≥0,
设x
1,x
2是此方程的两个根,
∴x
1•x
2=

=

,
∴

也是正整数,即m
2-1=1或2或3或6或9或18,
又m为正整数,
∴m=2;
(2)把m=2代入两等式,化简得a
2-4a+2=0,b
2-4b+2=0
当a=b时,

当a≠b时,a、b是方程x
2-4x+2=0的两根,而△>0,由韦达定理得a+b=4>0,ab=2>0,则a>0、b>0.
①a≠b,
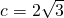
时,由于a
2+b
2=(a+b)
2-2ab=16-4=12=c
2故△ABC为直角三角形,且∠C=90°,S
△ABC=

.
②a=b=2-

,c=2

时,因

<

,故不能构成三角形,不合题意,舍去.
③a=b=2+

,c=2

时,因

>

,故能构成三角形.
S
△ABC=

×2

×

=

综上,△ABC的面积为1或

.
分析:(1)本题可先求出方程(m
2-1)x
2-3(3m-1)x+18=0的两个根,然后根据这两个根都是正整数求出m的值.
(2)由(1)得出的m的值,然后将m
2+a
2m-8a=0,m
2+b
2m-8b=0.进行化简,得出a,b的值.然后再根据三角形三边的关系来确定符合条件的a,b的值,进而得出三角形的面积.
点评:本题考查了一元二次方程根与系数的关系以及勾股定理等知识点,本题中分类对a,b的值进行讨论,并通过计算得出三角形的形状是解题的关键.

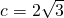 ,m2+a2m-8a=0,m2+b2m-8b=0.
,m2+a2m-8a=0,m2+b2m-8b=0. =
= ,
, 也是正整数,即m2-1=1或2或3或6或9或18,
也是正整数,即m2-1=1或2或3或6或9或18,
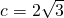 时,由于a2+b2=(a+b)2-2ab=16-4=12=c2
时,由于a2+b2=(a+b)2-2ab=16-4=12=c2 .
. ,c=2
,c=2 时,因
时,因 <
< ,故不能构成三角形,不合题意,舍去.
,故不能构成三角形,不合题意,舍去. ,c=2
,c=2 时,因
时,因 >
> ,故能构成三角形.
,故能构成三角形. ×2
×2 ×
× =
=
 .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案