搜索
【题目】如图，在Rt△ABC中，∠B=90°，∠ACB=45°，∠D=30°，B、C、D在同一直线上，连接AD，若AB= 
，则sin∠CAD= ． 
参考答案：
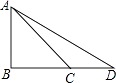
【答案】
【解析】解：∵在Rt△ABC中，∠B=90°，∠ACB=45°，
∴△ABC是等腰直角三角形，
∵AB= 
，
∴BC=AB= ，AC= 
AB= 
．
∵在Rt△ABD中，∠B=90°，∠D=30°，AB= ，
∴AD=2AB=2 ，BD= AB=3，
∴CD=BD﹣BC=3﹣ ．
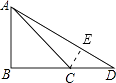
过C点作CE⊥AD于E．
∵S△ACD= 
ADCE= CDAB，
∴CE= 
= 
= 
，
∴sin∠CAD= 
= 
= ．
所以答案是 ．
【考点精析】掌握解直角三角形是解答本题的根本，需要知道解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC，D，E，F分别在三边上，且BE＝CD，BD＝CF，G为EF的中点．
(1)若∠A＝40°，求∠B的度数；
(2)试说明：DG垂直平分EF.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在△ABC中，∠BAC=90°，AB=AC，直线MN过点A且MN∥BC，点D是直线MN上一点，不与点A重合．
（1）若点E是图1中线段AB上一点，且DE=DA，请判断线段DE与DA的位置关系，并说明理由；
（2）请在下面的A，B两题中任选一题解答．
A：如图2，在（1）的条件下，连接BD，过点D作DP⊥DB交线段AC于点P，请判断线段DB与DP的数量关系，并说明理由；
B：如图3，在图1的基础上，改变点D的位置后，连接BD，过点D作DP⊥DB交线段CA的延长线于点P，请判断线段DB与DP的数量关系，并说明理由．
我选择： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一个整数能表示成a2+b2（a、b是正整数）的形式，则称这个数为“丰利数”．例如，2是“丰利数”，因为2=12+12，再如，M=x2+2xy+2y2=（x+y）2+y2（x+y，y是正整数），所以M也是“丰利数”．
（1）请你写一个最小的三位“丰利数”是 ，并判断20 “丰利数”．（填是或不是）；
（2）已知S=x2+y2+2x﹣6y+k（x、y是整数，k是常数），要使S为“丰利数”，试求出符合条件的一个k值（10≤k＜200），并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，BG⊥AC于G，DE⊥AB于E，DF⊥AC于F．
（1）在图（1）中，D是BC边上的中点，判断DE+DF和BG的关系，并说明理由．
（2）在图（2）中，D是线段BC上的任意一点，DE+DF和BG的关系是否仍然成立？如果成立，证明你的结论；如果不成立，请说明理由．
（3）在图（3）中，D是线段BC延长线上的点，探究DE、DF与BG的关系．（不要求证明，直接写出结果）
-
科目： 来源： 题型：
查看答案和解析>>【题目】小鹏和小娟玩一种游戏：小鹏手里有三张扑克牌分别是3、4、5，小娟有两张扑克牌6、7，现二人各自把自己的牌洗匀，小鹏从小娟的牌中任意抽取一张，小娟从小鹏的牌中任意抽取一张，计算两张数字之和，如果和为奇数，则小鹏胜；如果和为偶数则小娟胜．
（1）用列表或画树状图的方法，列出小鹏和小娟抽得的数字之和所有可能出现的情况；
（2）请判断该游戏对双方是否公平？并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一个点从数轴上的原点开始，先向左移动
到达
点，再向左移动
到达
点，然后向右移动
到达
点（1）用1个单位长度表示
，请你在数轴上表示出
、
、
三点的位置；
（2）把点
到点
的距离记为
，则
=_______ 
．（3）若点
以每秒
的速度向左移动，同时
、
点分别以每秒
、
的速度向右移动.设移动时间为
秒，试探索： 
的值是否会随着
的变化而改变？请说明理由．
相关试题
