
【题目】如图所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EF的长。
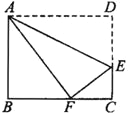
【答案】5cm.
【解析】试题分析:
设CE= ![]() ,则可得DE=
,则可得DE= ![]() ,由折叠的性质易得:AF=AD=BC=10,EF=DE=
,由折叠的性质易得:AF=AD=BC=10,EF=DE= ![]() ,在Rt△ABF中由勾股定理可得BF=6,从而可得FC=4,在Rt△EFC中由勾股定理建立方程,解方程即可求得
,在Rt△ABF中由勾股定理可得BF=6,从而可得FC=4,在Rt△EFC中由勾股定理建立方程,解方程即可求得![]() 得到CE的值.
得到CE的值.
试题解析:
∵四边形ABCD为矩形,
∴DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,
∵折叠矩形的一边AD,使点D落在BC边的点F处,
∴AF=AD=10,DE=EF,
在Rt△ABF中,BF=![]() =6,
=6,
∴FC=BC﹣BF=4,
设EC=x,则DE=8﹣x,EF=8﹣x,
在Rt△EFC中,
∵EC2+FC2=EF2,
∴x2+42=(8﹣x)2,解得x=3,
∴EC的长为3cm.
点睛;在这类有关矩形的折叠问题中,需注意两个问题:(1)折叠前后的两个对应图形是关于折痕对称的,要充分利用轴对称的性质;(2)把已知量和要求的量集中到一个直角三角形中,利用勾股定理建立方程来解题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2). 
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
①a>0;②b>0;③a+b+c>0;④2a+b=0;⑤方程ax2+bx+c=0的解为x1=﹣1,x2=3.
其中正确的是( )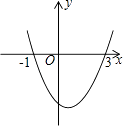
A.①②③
B.②③④
C.③④⑤
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1<![]() <2,所以
<2,所以![]() 的整数部分为1,将
的整数部分为1,将![]() 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分![]() -1,根据以上的内容,解答下面的问题:
-1,根据以上的内容,解答下面的问题:
(1)![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(2)1+![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(3)若设2+![]() 整数部分是x,小数部分是y,求x-y的值.
整数部分是x,小数部分是y,求x-y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
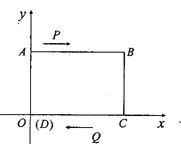
【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
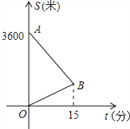
【题目】来自中国、美国、立陶宛、加拿大的四国青年男篮巅峰争霸赛于2014年3月25日-27日在我县体育馆举行。小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)从图中可知,小明家离体育馆 米,父子俩在出发后 分钟相遇.
(2)求出父亲与小明相遇时距离体育馆还有多远?
(3)小明能否在比赛开始之前赶回体育馆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为∠CAF的角平分线,BD=CD,∠DBC=∠DCB,∠DCA=∠ABD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com