
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
①a>0;②b>0;③a+b+c>0;④2a+b=0;⑤方程ax2+bx+c=0的解为x1=﹣1,x2=3.
其中正确的是( )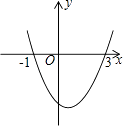
A.①②③
B.②③④
C.③④⑤
D.①④⑤
【答案】D
【解析】解:∵抛物线开口向上,
∴a>0,所以①正确;
∵抛物线的对称轴为直线x=﹣ ![]() >0,
>0,
∴b<0,所以②错误;
∵抛物线与x轴的交点在(﹣1,0)与(3,0),
∴当x=1时,y<0,
∴a+b+c<0,所以③错误;
∵抛物线与x轴的交点在(﹣1,0)与(3,0),
∴对称轴x= ![]() =1,
=1,
∴﹣ ![]() =1,
=1,
∴b=﹣2a,所以④正确;
∵抛物线与x轴的交点在(﹣1,0)与(3,0),
∴方程ax2+bx+c=0的解为x1=﹣1,x2=3,所以⑤正确.
故选D.
【考点精析】认真审题,首先需要了解二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)).


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC. 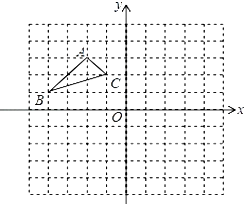
(1)作出△ABC关于x轴对称的△A1B1C1 , (只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2 , (只画出图形),写出B2和C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系(如图1),y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m. 
(1)求抛物线的解析式;
(2)现有一辆货运卡车,高4.4m,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双向道(如图2),为了安全起见,在隧道正中间设有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A.对角线互相垂直的平行四边形是正方形
B.相似三角形的周长之比等于相似的平方
C.若(1,y1)、(2,y2)是双曲线y=﹣ ![]() 上的两点,则y1<y2
上的两点,则y1<y2
D.方程x2﹣2x+3=0有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=4,E是BC上一点,将△CDE沿直线DE折叠后,点C落在点C′处,连接C′E交AD于点F,若BE=2,F为AD的中点,则AD的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年深圳国际马拉松赛于12月7日拉开帷幕,某马拉松爱好者用无人机拍摄比赛过程.如图,在无人机的镜头C下,观测深南大道A处的俯角为30°,B处的俯角为45°.如果此时无人机镜头C处离路面的高度CD为100米,点A、D、B在同一直线上,求A、B两处之间的距离. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com