
【题目】如图,在△ ABC中,AB=AC,点D在线段BC上,AD=BD,△ ADC是等腰三角形,求△ABC三个内角的度数。

【答案】∠BAC=108°,∠B=∠C=36°或∠BAC=90°,∠B=∠C=45°
【解析】
△ ADC是等腰三角形,分类讨论:分AC=DC或AD=DC两种情况;当AC=DC时,利用等腰三角形的等边对等角,设∠B![]() ,利用三角形的外角的性质求得∠ADC=∠B+∠BAD
,利用三角形的外角的性质求得∠ADC=∠B+∠BAD![]() ,然后利用三角形的内角和构建方程求解即可;当AD=DC时,利用等腰三角形的等边对等角结合三角形内角和定理即可求得答案.
,然后利用三角形的内角和构建方程求解即可;当AD=DC时,利用等腰三角形的等边对等角结合三角形内角和定理即可求得答案.
∵ △ ADC是等腰三角形
当AC=DC时
∴ ∠DAC=∠ADC
又∵ AB=AC,AD=BD
∴ ∠B=∠C=∠BAD
设∠B![]() ,则∠ADC= ∠B+∠BAD
,则∠ADC= ∠B+∠BAD![]()
∴∠DAC=∠ADC![]() ,∠BAC=∠DAC+∠BAD
,∠BAC=∠DAC+∠BAD![]()
于是在△ ABC中,有 ∠B+∠C+∠BAC![]() 180°
180°
解得![]()
所以,在△ ABC中,∠BAC=108°,∠B=∠C=36°
当AD=DC时,如下图:

∵AD=DC,
∴∠2=∠C,
∵AB=AC,
∴∠B=∠C
∵AD=BD,
∴∠B=∠1,
∴∠B=∠C=∠1=∠2,
∵∠B+∠C+∠1+∠2=180![]() ,
,
∴∠B+∠C=45![]() ,∠1+∠2=90°,
,∠1+∠2=90°,
∠BAC=∠1+∠2=90°,
所以,在△ ABC中,∠BAC=90°,∠B=∠C=45°


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD的面积为S,点P、Q时是ABCD对角线BD的三等分点,延长AQ、AP,分别交BC,CD于点E,F,连结EF。甲,乙两位同学对条件进行分析后,甲得到结论①:“E是BC中点” .乙得到结论②:“四边形QEFP的面积为![]() S”。请判断甲乙两位同学的结论是否正确,并说明理由.
S”。请判断甲乙两位同学的结论是否正确,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
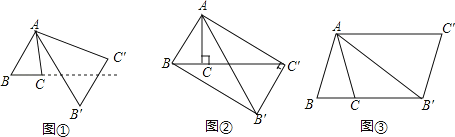
(1)如图①,对△ABC作变换[60°,![]() ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1且为实数),其中正确的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在坡角为30°的山坡上有一竖立的旗杆AB,其正前方矗立一墙,当阳光与水平线成45°角时,测得旗杆AB落在坡上的影子BD的长为8米,落在墙上的影子CD的长为6米,求旗杆AB的高(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,AB=AC,D点为Rt△ABC外一点,且BD⊥CD,DF为∠BDA的平分线,当∠ACD=15°,下列结论:①∠ADC=45°;②AD=AF;③AD+AF=BD;④BC﹣CE=2D,其中正确的是( )

A.①③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
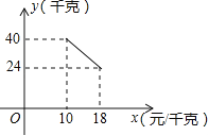
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com