解:∵四边形ABCD是正方形,
∴AB=AD=CD,∠A=∠ADC=90°,
∵E、F分别是边AB、AD的中点,
∴AE=BE=DF,
∵在△ADE和△DCF中,
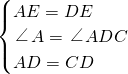
,
∴△ADE≌△DCF(SAS),
∴∠ADE=∠DCF,
∵∠ADE+∠CDE=∠ADC=90°,
∴∠DCF+∠CDE=90°,
∴∠CPD=180°-90°=90°,
∴∠CPG=90°,
∵G在CB的延长线上,
∴∠EBG=180°-∠ABC=180°-90°=90°,
∴∠A=∠EBG,
∵在△ADE和△BGE中,
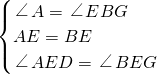
,
∴△ADE≌△BGE(ASA),
∴AD=BG,
∴PB是△PCG的中线,
∵正方形的边长为6cm,
∴CG=6+6=12cm,
∴PB=

CG=

×12=6cm.
分析:根据正方形的性质可得AB=AD=CD,∠A=∠ADC=90°,再根据中点定义求出AE=DF,然后利用“边角边”证明△ADE和△DCF全等,根据全等三角形对应角相等可得∠ADE=∠DCF,然后求出∠CDP=90°,再利用“角边角”证明△ADE和△BGE全等,根据全等三角形对应边相等可得AD=BG,从而求出PB是△PCG的中线,然后根据直角三角形斜边上的中线等于斜边的一半解答.
点评:本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半,熟练掌握各性质并求出三角形全都是解题的关键,难点在于要二次证明三角形全等.

 如图:已知E、F分别是正方形的边AB、AD中点,DE,CF相交于P,DE的延长线交CB的延长线于G,若正方形的边长为6cm,求PB的长.
如图:已知E、F分别是正方形的边AB、AD中点,DE,CF相交于P,DE的延长线交CB的延长线于G,若正方形的边长为6cm,求PB的长.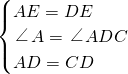 ,
,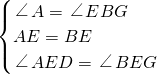 ,
, CG=
CG= ×12=6cm.
×12=6cm.

