
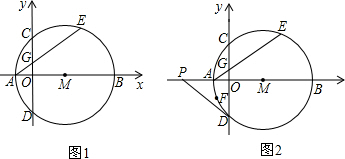
分析 (1)连接MC,构造直角三角形,利用勾股定理求得半径即可;
(2)首先利用垂径定理得到$\widehat{AD}$=$\widehat{AC}$,然后利用C为$\widehat{AE}$的中点得到$\widehat{AC}$=$\widehat{CE}$,从而得到$\widehat{AE}$=$\widehat{CD}$,利用等弧对等弦得到CD=AE即可;
(3)OF与OP的比例关系不变,在直角三角形DMP中,根据射影定理有DM2=MO•MP,①同理可求出OD2=OM•OP;
②然后分三种情况:
A:F与A重合时,OF=OA,PF=PA,可根据②求出OP的长根据①求出MP的长即可求出OP的长,进而可求出所求的比例关系;
B:F与B重合,同一;
C:F不与A、B重合.可通过相似三角形来求解.由于MF=DM,根据①可得出△OMF与△FMP相似,可得出$\frac{OF}{PF}$=$\frac{MO}{MF}$=$\frac{3}{5}$.
综合三种情况即可得出OF:PF的值.
解答 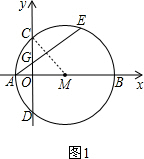 解:(1)如图1,连接MC,
解:(1)如图1,连接MC,
设半径AM=CM=r,则OM=r-2,
由OC2+OM2=MC2得:
42+(r-2)2=r2,
解得:r=5,
故⊙M的半径为5;
(2)∵直径AB⊥CD,
∴CO=OD,
∴$\widehat{AD}$=$\widehat{AC}$,
∵C为$\widehat{AE}$的中点,
∴$\widehat{AC}$=$\widehat{CE}$,
∴$\widehat{AE}$=$\widehat{CD}$,
∴CD=AE=8;
(3)如图2,连接DM,则DM⊥PD,DO⊥PM,
∴△MOD∽△MDP,△MOD∽△DOP,
∴DM2=MO•MP;
DO2=OM•OP,
即42=3•OP,
∴OP=$\frac{16}{3}$.
当点F与点A重合时:$\frac{OF}{PF}$=$\frac{AO}{AP}$=$\frac{2}{\frac{16}{3}-2}$=$\frac{3}{5}$,
当点F与点B重合时:$\frac{OF}{PF}$=$\frac{OB}{PB}$=$\frac{8}{\frac{16}{3}+8}$=$\frac{3}{5}$,
当点F不与点A、B重合时:连接OF、PF、MF,
∵DM2=MO•MP,
∴FM2=MO•MP,
∴$\frac{FM}{OM}$=$\frac{MP}{FM}$,
∵∠AMF=∠FMA,
∴△MFO∽△MPF,
∴$\frac{OF}{PF}$=$\frac{MO}{MF}$=$\frac{3}{5}$.
∴综上所述,$\frac{OF}{PF}$的比值不变,比值为$\frac{3}{5}$.
点评 本题考查了圆的综合知识、相似三角形的判定与性质等知识,解题的关键是得到△MOD∽△MDP,△MOD∽△DOP,从而得到DM2=MO•MP,综合性较强,难度较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
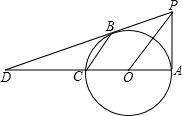 以AC=6为直径画一个圆,过点A作AP⊥AC,过点C作CB∥OP,直线PB与直线AC相交于点D.
以AC=6为直径画一个圆,过点A作AP⊥AC,过点C作CB∥OP,直线PB与直线AC相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
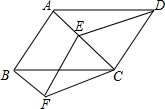 已知:如图,在四边形ABCD中,AB∥CD,点E是对角线AC上一点,∠DEC=∠ABC,且CD2=CE•CA.
已知:如图,在四边形ABCD中,AB∥CD,点E是对角线AC上一点,∠DEC=∠ABC,且CD2=CE•CA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com