
 小明同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先画出了如图的四边形ABCD,并写出了如下不完整的已知和求证.
小明同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先画出了如图的四边形ABCD,并写出了如下不完整的已知和求证. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,∠ACB=30°,则BD的长是( )
如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,∠ACB=30°,则BD的长是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{7}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
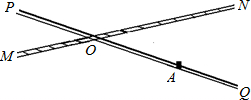 如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为多少?
如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线相等且互相垂直的四边形是菱形 | |
| D. | 对角线相等且互相垂直的平行四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
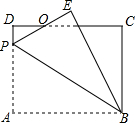 如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )
如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为( )| A. | 4.8 | B. | 3$\sqrt{2}$ | C. | 5 | D. | 3$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com