
【题目】用适当的方法解下列方程:
(1) ![]() (2)2x2+3x—1=0(用配方法解)
(2)2x2+3x—1=0(用配方法解)
(3) ![]() (4)(x+1)(x+8)=-2
(4)(x+1)(x+8)=-2
(5) ![]() (6)
(6) ![]()
【答案】(1)x1=0,x2=4;(2)x1=![]() ,x2=
,x2=![]() ;(3)x1=2,x2=3;(4)x1=
;(3)x1=2,x2=3;(4)x1=![]() ,x2=
,x2=![]() ;(5)x1=1,x2=—2;(6)
;(5)x1=1,x2=—2;(6)![]() ,
,![]() .
.
【解析】(1)方程变形后,开方即可求出解;(2)利用配方法解方程,先将系数化为1,再将方程两边同时加一次项系数一半的平方,即可求解;(3)先移项,再提公因式化为两个因式相乘的形式,进而求解;(4)首先整理,然后找出a、b、c的值,利用求根公式得出答案;(5)设y=x+x,则原方程可化为2y-3=![]() ,解方程求得y的值,再代入x+x=y,求出x的值即可;(6)利用代入法求解即可.
,解方程求得y的值,再代入x+x=y,求出x的值即可;(6)利用代入法求解即可.
(1) ![]() ,
,
变形得:![]() ,
,
开方得:x-2=2或x-2=-2,
解得: x1=0,x2=4;
(2)解:![]() ,
,
![]() ,
,![]() ,(x+
,(x+![]() )=
)=![]() ,x+
,x+![]() =±
=±![]() ,
,
![]() ,
,![]() .
.
(3)![]() ,(x-2)(3x-6-x)=0,即x-2=0或3x-6-x=0,解得:x1=2,x2=3.
,(x-2)(3x-6-x)=0,即x-2=0或3x-6-x=0,解得:x1=2,x2=3.
(4) (x+1)(x+8)=-2,x+9x+10=0, 由a=1,b=9,c=10, ∵b-4ac=81-40=41,
∴x=![]() ∴x1=
∴x1=![]() ,x2=
,x2=![]() .
.
(5) ![]() ,设x+x=y, 则2y-3=
,设x+x=y, 则2y-3=![]() , 2y-3y=2,(y-2)(2y+1)=0,
, 2y-3y=2,(y-2)(2y+1)=0,![]() ,
,
当x+x=2,解得:x1=1,x2=—2 ;当x+x=![]() ,2x+2x+1=0,b-4ac<0, ∴此方程无解;
,2x+2x+1=0,b-4ac<0, ∴此方程无解;
经检验原方程的解为:x1=1,x2=—2;
(6)![]() ,由①得y=x-3③,把③代入②得:x+x-2=0,解得
,由①得y=x-3③,把③代入②得:x+x-2=0,解得![]() .分别代入③得
.分别代入③得![]() ,∴原方程的解为:
,∴原方程的解为:![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2), 
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组计划做一批“中国结”,如果每人做5个,那么比计划多了9个;如果每人做4个,那么比计划少15个.该小组共有多少人?计划做多少个“中国结”?
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明:5x□( )=4x□( ); 小红:![]() .
.
(1)根据小明、小红所列的方程,其中“□”中是运算符号,“( )”中是数字,请你分别指出未知数x、y表示的意义.
小明所列的方程中x表示 ,
小红所列的方程中y表示 ;
(2)请选择小明、小红中任意一种方法,完整的解答该题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: 
(1)本次调查的学生共有人,在扇形统计图中,m的值是;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E,F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[k-1,k2-1]的一次函数为正比例函数,求k的值;
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且△OAB的面积为4(O为原点),若一次函数的图象过A,B两点,求该一次函数的特征数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )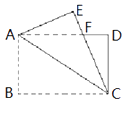
A. ![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com