
分析 (1)根据边角边公理证明;
(2)过A作AM∥BC,交EF与D,证明△PAD≌△PCF,根据全等三角形的性质进行比较即可;
(3)延长CP到点C',使得PC=PC',过点C'作AB∥OM,过P作任意直线EF,交AB于D,交ON于E,交OM于F,证明△PCF≌△PC'D,根据勾股定理计算即可.
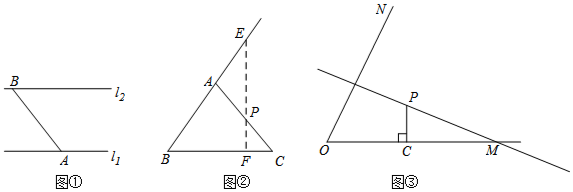
解答 解:(1)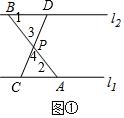 如图①,在△APC和△BPD中,
如图①,在△APC和△BPD中,
∵$\left\{\begin{array}{l}∠1=∠2\\ AP=BP\\∠3=∠4\end{array}\right.$
∴△APC≌△BPD;
(2)S△PEC=S△PAE∴S△APC=A△BPD.
如图②,过A作AD∥BC,交EF与D,
∵P为AC中点,
∴PA=PC,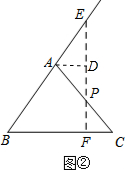
∵AD∥BC,
∴∠PAD=∠C
在△PAD和△PCF中,
∵$\left\{\begin{array}{l}{∠PAD=∠C}\\{∠APD=∠CPF}\\{PA=PC}\end{array}\right.$,
∴△PAD≌△PCF(ASA),
∴S△PAD=S△PCF
∴S△PAD+S△EAD>S△PCF
即S△PFC<S△PAE;
(3)如图③,延长CP到点C',使得PC=PC',
过点C'作AB∥OM,过P作任意直线EF,交AB于D,交ON于E,交OM于F,
∵AB∥OM,
∴∠F=∠1,
在△PCF和△PC'D中,
∵$\left\{\begin{array}{l}{∠F=∠1}\\{∠DPC′=∠FPC}\\{PC=PC′}\end{array}\right.$,
∴△PCF≌△PC'D(ASA),
∴S△PCF=S△PC'D.
∵S△EOF=S△ADE+S四边形AOFD=S△ADE+S五边形AOCPD+S△POF=S△ADE+S五边形AOCPD+S△PO'DS△ADE+S四边形AOCC′,
∴当S△ADE=0时,S△EOF最小.
过A作AG⊥OM于G,则AG=CC'=3+3=6,
在 Rt△AOG中,
∵∠OAG=90°-60°=30°,
∴设OG=x,则OA=2x.
∵OG2+AG2=OA2
∴x2+62=4x2
∴$x=2\sqrt{3}$,即$OG=2\sqrt{3}$,
∴$CG=OC-OG=6\sqrt{3}-2\sqrt{3}=4\sqrt{3}$.
∴$AC'=CG=4\sqrt{3}$,
∴${S_{△EOF最小值}}={S_{四边形AOCC'}}=\frac{1}{2}×(OC+AC')×AG$=$\frac{1}{2}×(6\sqrt{3}+4\sqrt{3})×6=30\sqrt{3}$.
点评 本题考查的是全等三角形的判定和性质、最短路径问题,掌握全等三角形的判定定理和性质定理是解题的关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:解答题
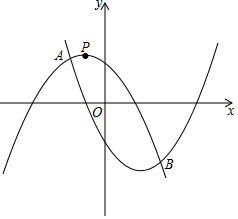 如图所示,抛物线y1=-ax2+(a-1)x+1经过点P(-$\frac{1}{3}$,$\frac{10}{9}$),且与抛物线y2=ax2-(a+1)x-1相交于A,B两点.
如图所示,抛物线y1=-ax2+(a-1)x+1经过点P(-$\frac{1}{3}$,$\frac{10}{9}$),且与抛物线y2=ax2-(a+1)x-1相交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走( )米才最理想.
主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她至少走( )米才最理想.| A. | 18-6$\sqrt{5}$ | B. | 6$\sqrt{5}$-6 | C. | 6$\sqrt{5}$+6 | D. | 18-6$\sqrt{5}$或6$\sqrt{5}$-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3(x+3)2-2 | B. | y=3(x+3)2+2 | C. | y=3(x+2)2+3 | D. | y=3(x-2)2+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com