
【题目】作图题
(1)如图,已知∠AOB和C、D两点,在∠AOB内部找一点P,使PC=PD,且P到∠AOB的两边OA、OB的距离相等.

(2)如图,在长度为1个单位长度的小正方形组成]的正方形网格中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线l成轴对称的△A′B′C′;
②在直线l上找一点P(在答题纸上图中标出),使PB+PC的长最短;

 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点,CE⊥BD于E.

(1)如图(1),若BD平分∠ABC时,①求∠ECD的度数;②延长CE交BA的延长线于点F,补全图形,探究BD与EC的数量关系,并证明你的结论;
(2)如图(2),过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=ax![]() +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x![]() -3x+5,则a+b+c=__________。
-3x+5,则a+b+c=__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节小明妈妈包了4个蛋黄棕子,6个八宝棕子,10个红枣棕子,从外观上看,它们都一样,
(1)小明吃一个就能吃到黄棕子的概率是多少?
(2)如果爸爸、妈妈每人吃了3个粽子,都没有吃到蛋黄粽子,之后,小明吃一个就吃到蛋黄粽子的概率是多少?如果小明第一个真的吃到了一个蛋黄粽子,那么他再吃一个依然吃到蛋黄粽子的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字:![]() ,1,2,
,1,2,![]() 的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法![]() 只选其中一种
只选其中一种![]() ,表示两次抽出卡片上的数字的所有结果;
,表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点![]() 落在双曲线
落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:

①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从德州市2013年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根据检测数据制作了尚不完整的频数分布表和条形图:
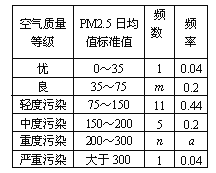
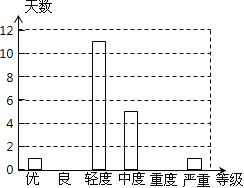
(1)求出表中m,n,a的值,并将条形图补充完整;
(2)以这25天的PM2.5日均值来估计该年的空气质量情况,估计该年(365天)大约有多少天的空气质量达到优或良;
(3)请你结合图表评价一下我市的空气质量情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的题目及分析过程.已知:如图点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]()



原图 ① ②
说明:![]()
说明两个角相等,常用的方法是应用全等三角形或等腰三角形的性质.观察本题中说明的两个角,它们既不在同一个三角形中,而且们所在两个三角形也不全等.因此,要说明![]() ,必须添加适当的辅助线,构造全等三角形或等腰三角形,现在提供两种添加辅加线的方法如下:
,必须添加适当的辅助线,构造全等三角形或等腰三角形,现在提供两种添加辅加线的方法如下:
如图①过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
如图②延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)请从以上两种辅助线中选择一种完成上题的说理过程.
(2)在解决上述问题的过程中,你用到了哪种数学思想?请写出一个._______________.
(3)反思应用:

如图,点![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() .
.
请类比(1)中解决问题的思想方法,添加适当的辅助线,判断线段![]() 与
与![]() 之间的大小关系,并说明理由.
之间的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com