
 A在x轴上,点C在y轴上,OC=
A在x轴上,点C在y轴上,OC= ,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE. ∠OCA=30°,
∠OCA=30°, ×
× =1,
=1, ),E(1,0)代入得
),E(1,0)代入得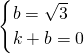 ,
, ,
, x+
x+ .
. =2
=2 ,
, =3,
=3, ,
, -
- =
= ,
, ,
, ,
, .
. ,
, ).
).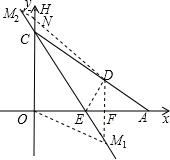 第一种情况:此点在第四象限内,设为M1,延长DF交直线CE于M1,
第一种情况:此点在第四象限内,设为M1,延长DF交直线CE于M1, ,
, ,y1),
,y1), x+
x+ 中,
中, ×
× +
+ =-
=- ,即FM1=
,即FM1= .
. ,-
,- ),
), +
+ =
= ,OC=
,OC= ,
, ,
, ,
, ,
, ×
× =
= ,
, ×
× =
= ,
, ,
, ,
, ),
), ,-
,- ),M2(-
),M2(- ,
, ).
). ∠OCA=30°,
∠OCA=30°, ×
× =1,从而可求点E的坐标是(1,0).
=1,从而可求点E的坐标是(1,0). ,所以C(0,
,所以C(0, ).
). ,可求出AD=AC-CD=2
,可求出AD=AC-CD=2 -
- =
= .
. ,AF=AD•cos∠CAO=
,AF=AD•cos∠CAO= ,所以OF=AO-AF=
,所以OF=AO-AF= ,从而点D的坐标是(
,从而点D的坐标是( ,
, );
); ,所以可设点M1的坐标为(
,所以可设点M1的坐标为( ,y1),利用点M1在直线CE上,可得y1的值,即可求出点M1的坐标是(
,y1),利用点M1在直线CE上,可得y1的值,即可求出点M1的坐标是( ,-
,- ),所以有DM1=DF+FM1=
),所以有DM1=DF+FM1= +
+ =
= ,OC=
,OC= ,所以DM1=OC.
,所以DM1=OC. ,
, ,所以CN=
,所以CN= .
. 可得M2(-
可得M2(- ,
, ).
).

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 3 |
| 3 |
 在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
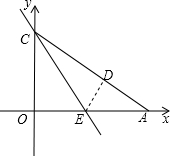 A在x轴上,点C在y轴上,OC=
A在x轴上,点C在y轴上,OC=| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC=
如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC=| 3 |
查看答案和解析>>
科目:初中数学 来源:2010年浙江省舟山市初中毕业生学业水平考试调研试卷(解析版) 题型:解答题
 ,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
查看答案和解析>>
科目:初中数学 来源:2005年辽宁省沈阳市中考数学试卷(课标卷)(解析版) 题型:解答题
 ,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30度.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com